V článku o odvození rovnice ideálního plynu jsme nakousli několik termodynamických zákonitostí, nicméně bylo by dobré, abychom se na termodynamiku podívali i trochu obecněji a do hloubky.
Rovnici idálního plynu jsme si již odvodili, nyní však pro připomenutí:
$$PV=nRT$$
kde \(P\) odpovídá tlaku plynu, \(V\) jeho objemu, \(n\) molárnímu množství plynu, \(R\) je plynová konstanta a \(T\) odpovídá teplotě plynu.
Dále využijeme 1. termodynamického zákona, který nám stručně říká, že změna vnitřní energie nějaké soustavy odpovídá součtu změn práce a přijatého tepla, tedy[1]Další informace kupříkladu na http://fyzika.jreichl.com/main.article/view/581-prvni-termodynamicky-zakon :
$$\mathrm{d}u = \mathrm{d}w + \mathrm{d}q$$
Využijme těchto znalostí při prohlídce obyčejného pístu a válce:
Zeleně je zobrazen nějaký (ideální) plyn, šedivě potom píst, černé jsou kontury. Představme si nyní situaci, kdy plyn trošku “přimáčkneme”:
Pokud budeme působit nějakou silou \(F\) na danou plochu \(A\), víme, že tvoříme nějaký tlak, konkrétně tedy \(P = \frac{F}{A}\). Taktéž víme, že práce \(w\) odpovídá síle \(F\) po nějaké dráze \(l\), tedy \(W = F \cdot l\).
Budeme-li se zajímat pouze o drobnou změnu práce, tedy \(\mathrm{d}w\), poté můžeme psát:
$$\mathrm{d}w = F \cdot \mathrm{d}l$$
Výše jsme si řekli, že \(P = \frac{F}{A}\), tedy \(F = P A\), můžeme tedy dosadit:
$$\mathrm{d}w = P A \cdot \mathrm{d}l$$
Nu a do jsme se učili už na základní škole o ploše a výšce? Vynásobíme-li je, dostaneme objem! Takže vzhůru do toho:
$$\mathrm{d}w = P \cdot \mathrm{d}V$$
Správněji tedy \(\mathrm{d}w = {- P} \cdot \mathrm{d}V\), protože \(\mathrm{d}l\) zde objem snižuje a ne zvyšuje (tedy správně bychom od začátku měli psát \({-\mathrm{d}l}\), ale je doufám jasné, kde se vzalo. Také vidíme důležitý závěr: Pokud se nezmění objem, není práce[2]Zde by to chtělo podotknout, že mluvíme samozřejmě o fyzikální práci. Takže pokud jste nezaměstnaní a zhubnete, práci nedostanete 🙂 .
První termodynamický zákon tedy můžeme přepsat jako:
$$\mathrm{d}u = \mathrm{d}q – P \mathrm{d}V$$
Můžeme tedy tvrdit, že energie je funkcí teploty a objemu[3]Proč ne tlaku? Tlak je totiž definován pomocí těchto dvou veličin (není to nezávislá veličina). Proto tedypouze teplota a objem.:
$$u = f(T, V)$$
konkrétněji tedy:
$$\mathrm{d}u = \left(\frac{\partial u}{\partial T}\right)_{V} \mathrm{d}T + \left(\frac{\partial u}{\partial V}\right)_{T} \mathrm{d}V $$
To znamená, že změna energie se dá popsat jako parciální derivace energie vzhledem k teplotě, pokud zachováme konstantní objem, krát změna teploty, plus parciální derivace energie vzhledem k objemu, pokud zachováme konstantní teplotu, krát změna objemu.
Nicméně — podívejme se nyní na druhou část zlomku. Pokud je objem konstantní, poté \(\mathrm{d}V\) je nulové (změna \(V\) je nulová), proto nám tedy celá druhá část zlomku vypadne a můžeme psát:
$$\mathrm{d}u = \mathrm{d}q + \mathrm{d}w = \mathrm{d}q + 0 = \mathrm{d}q = \left(\frac{\partial u}{\partial T}\right)_{V} \mathrm{d}T$$
Poslední části “před” \(\mathrm{d}T\), tedy \(\left(\frac{\partial u}{\partial T}\right)_{V} = C_V\) říkáme tepelná kapacita při konstantním objemu. Tedy:
$$\mathrm{d}u = \mathrm{d}q = C_V \mathrm{d}T$$
To vše jsme si definovali, abychom si mohli definovat následující termín:
Entropie
Než tak však učiníme, definujme si ještě tzv. entalpii. Označíme ji velkým písmenem \(H\) a bude pro ni platit[4]Více informací: http://scienceworld.wolfram.com/physics/Enthalpy.html:
$$ H = u + P V $$
Entalpie je tedy funkcí teploty a tlaku, tedy \(H = f(T, P)\). Podle prvního termodynamického zákona[5]dále jen TZ1 jsme si ukázali:
$$ \mathrm{d}u = \mathrm{d}q + \mathrm{d}w = \mathrm{d}q – P \mathrm{d}V$$
Můžeme tedy trošku popřeházet písmenka, aby:
$$ \mathrm{d}u + P \mathrm{d}V = \mathrm{d}q$$
a tedy
$$ \mathrm{d} (u+PV) = \mathrm{d}q $$
čili
$$ \mathrm{d}H = \mathrm{d}q $$
Vidíme, že tedy entalpie je funkcí teploty a tlaku, tedy \(H(T,P)\). A můžeme samozřejmě opět vytvořit parciální derivace:
$$ \mathrm{d}H = \left(\frac{\partial H}{\partial T}\right)_P \mathrm{d}T + \left(\frac{\partial H}{\partial P}\right)_T \mathrm{d}P = \mathrm{d}q$$
Nu a opět, pokud uvažujeme konstantní tlak, celé \(\mathrm{d}P\) bude nulové, čili:
$$ \mathrm{d}H = \left(\frac{\partial H}{\partial T}\right)_P \mathrm{d}T = \mathrm{d}q$$
Části \(\left(\frac{\partial H}{\partial T}\right)_P\) říkáme tepelná kapacita při konstantním tlaku. A můžeme si (po přeházení písmenek) ukázat, že:
$$ \mathrm{d}q = C_p \mathrm{d}T$$
Shrňme si nyní, co víme: Víme \(C_p\), \(C_V\), známe vzorec pro entalpii. Zkusme si s ním nyní trošku pohrát:
$$ H = u + PV $$
$$ \left(\frac{\partial H}{\partial T}\right)_p = \left(\frac{\partial u}{\partial T}\right)_p + \left(\frac{\partial PV}{\partial T}\right)_p $$
Vidíme, že pokud bychom derivovali (parciálně) při konstantním tlaku, poslední část, kde bychom derivovali i tlak samotný, by se převedla na \(\left(\frac{P \mathrm{d}V}{\mathrm{d}T}\right)_p\), tedy:
$$ \left(\frac{\partial H}{\partial T}\right)_p = \left(\frac{\partial u}{\partial T}\right)_p + \left(\frac{P \mathrm{d}V}{\mathrm{d}T}\right)_p $$
Vrátíme-li se na chvilku zpět k rovnici ideálního plynu, tedy \(PV = nRT\), pokud trošku přeházíme písmenka a vyjádříme jako diferenciály:
$$ \frac{\mathrm{d}V}{\mathrm{d}T} = \frac{nR}{P} $$
Pro zjednodušení předpokládejme, že \(n=1\), čili:
$$ \frac{\mathrm{d}V}{\mathrm{d}T} = \frac{R}{P} $$
a tedy
$$ \frac{P \mathrm{d}V}{\mathrm{d}T} = R $$
Vidíme, že to je to, co nám vyšlo výše jako jeden z členů součtu — můžeme tedy dosadit do vzorce výše to, co už známe:
$$ C_p = \left(\frac{\partial u}{\partial T}\right)_p + R $$
Nicméně abychom “minimalizovali” i tento vzorec, museli bychom mít konstantní jinou veličinu. Pokud máme konstantní tlak, tak změna objemu podle teploty není to, co by se nám zrovna hodilo. Ale už jsme “skoro” tam, musíme akorát udělat malý trik. Využijeme “řetězového zákona”[6]Nevím, jak to lépe přeložit, každopádně další informace o tom zde: http://en.wikipedia.org/wiki/Triple_product_rule.. A ten nám neříká nic jiného, že naši parciální derivaci při konstantním tlaku můžeme rozepsat následovně:
$$ \left(\frac{\partial u}{\partial T}\right)_p = \left(\frac{\partial u}{\partial T}\right)_V + \left[\left(\frac{\partial u}{\partial V}\right)_T\right] \left(\frac{\partial V}{\partial T}\right)_p $$
Podívejme se nyní na třetí závorku, resp. druhou, jdeme-li od rovnítka vpravo (zvýraznil jsem ji hranatými závorkami). Ta operuje se změnou energie při konstantní teplotě. Nicméně výše jsme si řekli, že pokud je konstantní teplota, nejde žádná energie dovnitř ani ven[7]Tzn. jedná se o dokonalý stroj, který převádí tepelnou energii na energii pohybu pístu třeba — sice je to ideální zařízení, ale nám se to teď dost hodí.. Změna energie je tedy nulová — čímž i součin je nulový a celá poslední část vzorce “vypadne”.
Položíme proto rovnost:
$$ \left(\frac{\partial u}{\partial T}\right)_p = \left(\frac{\partial u}{\partial T}\right)_V $$
čímž si značně zjednodušíme práci s výrazem výše. Můžeme totiž poslední část nazvat \(C_V\), čili tepelnou kapacitu při konstantním objemu. A tedy samozřejmě pak platí, že:
$$ C_p = C_V + R $$
Podívejme se nyní, co tedy již víme:
$$ \mathrm{d}u = \mathrm{d}q + \mathrm{d}w = \mathrm{d}q + p\mathrm{d}V = C_V \mathrm{d}T $$
Na tom dále vystavíme[8]a již brzy se dostaneme ke slíbené entropii, slibuji 🙂 , nicméně musíme se podívat na další “kus” informací ze světa termodynamiky — různé procesy. Určitě jste o nich už někdy slyšeli, ale pro zopakování si napíšeme malý seznam:
- isotermický děj je takový, během kterého zůstává stejná teplota
- isobarický děj je takový děj, během něhož zůstává konstantní tlak
- isochodirký děj takový, kdy zůstává konstantní objem
- isentalpický děj — zůstává zachována entalpie
Kromě těchto tří existují ještě isentropický děj, kde zůstává zachována entropie. Zatím však nevíme, co to je, nebudu ho tam uvádět[9]A samozřejmě až budete vědět, co to je a jak je definováno, můžete si to tam virtuálně přiřadit. Zbývá však jeden, na který se ještě musíme podívat — děj adiabatický.
Adiabatický děj
Adiabatický děj je takový, během něhož zůstává celkové teplo[10]pozor, nokoliv teplota!! děje konstantní. Samozřejmě se může měnit leccos ostatního, včetně teploty, ale teplo systému je konstantní. Jak je to možné?
Můžeme náš testovací systém třeba dokonale (či co nejdokonaleji) odizolovat od okolního světa. Důležité je, že žádné teplo nejde ani dovnitř, ani ven. Můžeme tedy tvrdit, že \(\mathrm{d}q = 0\). Podívejme se ještě jednou na vztah:
$$\mathrm{d}u=\mathrm{d}q-p\mathrm{d}V=C_V\mathrm{d}T$$
Řekli jsme si, že \(\mathrm{d}q=0\), čili můžeme tento člen s klidným svědomím vypustit:
$$\mathrm{d}u={-p}\mathrm{d}V=C_V\mathrm{d}T$$
Tlak \(p\) si můžeme vyjádřit z nám již známého $pV=nRT$:
$$ p=\frac{nRT}{V} $$
A můžeme tedy dosadit:
$$\mathrm{d}u = {-\frac{nRT}{V}}\mathrm{d}V = C_V \mathrm{d}T$$
a po trošku úpravách[11]Jen přeházíme “sem a tam” přes rovnítko různé proměnné tak, aby nám na jedné straně u sebe zbyly diferenciály a proměnné teploty, na druhé objemu. získáme:
$$ {-nR}\frac{\mathrm{d}V}{V}=\frac{C_V\mathrm{d}T}{T} $$
Samozřejmě budeme považovat opět \(n=1\)[12]molární množství látky, takže se to celé zjednoduší na:
$$ {-R}\frac{\mathrm{d}V}{V}=\frac{C_V\mathrm{d}T}{T} $$
Menší už to snad ani nemůže být, máme připraveno na integrování. Integrování je matematická operace inverzní k derivování (a parciálnímu derivování), pokud bude zájem, o těchto metodách zvlášť napíšu článek. Napíšeme tedy:
$$ {-R}\int_{V_1}^{V_2}\frac{\mathrm{d}V}{V} = {C_V}\int_{T_1}^{T_2}\frac{\mathrm{d}T}{T}$$
a zintegrujeme. Funkce \(\frac{1}{x}\) se zintegruje na \(ln(x) +C\), tedy rozintegrované bude:
$$ {-R}\left[\ln(V)\right]_{V_1}^{V_2} = C_V \left[\ln(T)\right]_{T_1}^{T_2}$$
Po dosazení[13]Jak na to se dozvíte v tom slibovaném článku o integrálech, ale když se na to zakoukáte, vymyslíte to 🙂 bude:
$$ {-R}\left(\ln(V_2)-\ln(V_1)\right) = C_V \left( \ln(T_2)-\ln(T_1)\right) $$
Podle pravidel o logaritmování tedy:
$$ {-R}\ln\frac{V_2}{V_1} = C_V \ln \frac{T_2}{T_1}$$
A abychom se zbavili “mínus” před \(R\), stačí si představit, jak by to vypadalo, pokud bych se ho zbavil již výše, než jsem použil pravidla o logaritmování — otočilo by se pouze pořadí, tedy:
$$ {R}\ln\frac{V_1}{V_2} = C_V \ln \frac{T_2}{T_1}$$
Dále použiji pravidla o logaritmování součinu, který se v logaritmu převede na mocninu. Takže vzhůru do toho:
$$ \ln\left(\frac{V_1}{V_2}\right)^{R} = \ln \left( \frac{T_2}{T_1} \right)^{C_V}$$
Pokud se podíváme, je jasné, že aby toto platilo, musí se “vnitřky závorek” mezi sebou rovnat (závorka vpravo a závorka vlevo). Můžeme tedy napsat:
$$ \ln\left(\frac{V_1}{V_2}\right)^{\frac{R}{C_V}} = \ln \left( \frac{T_2}{T_1} \right)$$
A tedy i:
$$\left(\frac{V_1}{V_2}\right)^{\frac{R}{C_V}} = \frac{T_2}{T_1}$$
Vzpomeňme si nyní na vztah:
$$C_P = C_V + R$$
Není vám to povědomé? 🙂 Z toho přece můžeme snadno vyjádřit \(R\):
$$R = C_P – C_V$$
a tedy (celý vztah podělíme \(C_V\))
$$ \frac{R}{C_V} = \frac{C_P}{C_V} – \frac{C_V}{C_V}$$
A to samozřejmě můžeme pokrátit na
$$ \frac{R}{C_V} = \frac{C_P}{C_V} – 1$$
Abychom si trošku zjednodušili práci (dobře, abych si ji zjednodušil já, nebaví mě psát v \(\LaTeX\)u zlomky 😀 ), nazvu pro teď výraz \(\frac{C_V}{C_P}=\xi\)[14]Tuten paznak se čte jako “ksí”. Pak samozřejmě platí, že:
$$ \frac{R}{C_V} =\xi-1$$
Samozřejmě tedy můžeme původní vztah přepsat jako:
$$\left(\frac{V_1}{V_2}\right)^{\xi-1} =\frac{T_2}{T_1} $$
Vraťme se nyní zpět k rovnici ideálního plynu:
$$ PV = nRT$$
a vyjádřeme si \(T\), položmě \(n=1\) jako před tím:
$$ T = \frac{PV}{R}$$
Dosaďme nyní do nově vzniknuvšího vztahu:
$$\left(\frac{V_1}{V_2}\right)^{\xi-1} =\frac{\frac{P_2V_2}{R}}{\frac{P_1V_1}{R}} $$
Samozřejmě můžeme s klidným svědomím pokrátit \(R\):
$$\left(\frac{V_1}{V_2}\right)^{\xi-1} =\frac{{P_2V_2}}{{P_1V_1}} $$
Nyní se můžeme snadno zbavit \(V_1\) a \(V_2\) — přendáme je na druhou stranu, čili:
$$\frac{V_1}{V_2} \left(\frac{V_1}{V_2}\right)^{\xi-1} =\frac{P_2}{P_1} $$
což samozřejmě přepíšeme na:
$$\left(\frac{V_1}{V_2}\right)^{\xi}=\frac{P_2}{P_1} $$
Z toho snadno vyjádříme:
$$P_1V_1^{\xi}=P_2V_2^{\xi} $$
Vidíme, že pokud se musí rovnat levá a pravá strana rovnice, musí být konstantní obecný výraz \(\left(PV\right)^\xi\).
Zpátky však k entropii!
Nyní, když už rozumíme adiabatickému ději, máme téměř všechny důležité informace k tomu, abychom mohli vyjádřit a pochopit i termín entropie. Začněme se tedy věnovat tepelným procesům, konkrétně tzv. Carnotovu [15]Informace např. zde: http://www-history.mcs.st-andrews.ac.uk/Biographies/Carnot_Sadi.html cyklu[16]Moc hezké informace a interaktivní aplety mají třeba zde: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/carnot.html.
Carnot si položil jednoduchou otázku: Existuje-li nějaký tepelný zdroj, tak máme-li nějakou možnost vzít nějaký přístroj (obecně tepelný stroj), který je schopen teplo tohoto zdroje převádět na práci, pokud možno 100% efektivně. A ukázalo se, že nikoliv[17]Dnes nám to už může přijít jako samozřejmost, ale stejně po světě běhá spoustu lidí, co si myslí, že vynalezlo perpetum mobile, což jeho existenci přímo jako důsledek tohoto zjištění vyvrací.
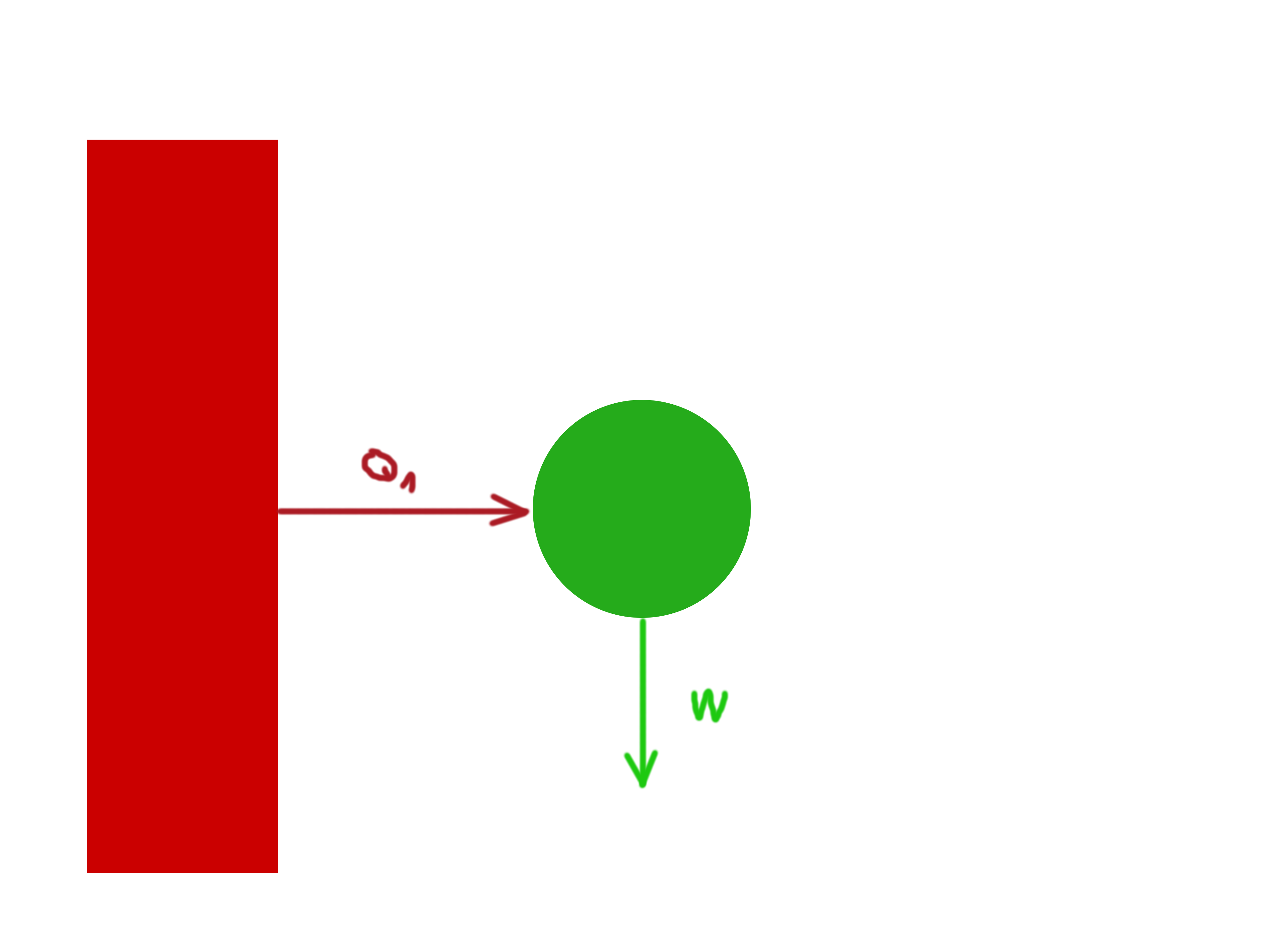
Vezmeme-li tedy nějaký tepelný zdroj:
Přidáme stroj, který má toto teplo zpracovávat:
Tak se ptáme, jestli existuje takový stroj, který je schopen 100% přenést veškeré teplo na práci, tedy že pracuje se 100% účinností:
Ukázalo se však, že takový stroj může existovat pouze v ideálních podmínkách, nicméně ty nejsou dosažitelné. Každý takový stroj totiž operuje i se zbytkovým teplem, které je předáváno dál okolí:
Nyní si vše ukažme trošku exaktněji:
Ze “situačního plánku” vidíme, že výstupní práce \(W\) bude rovna rozdílu \(W=Q_1 – Q2\). Víme taktéž, že efektivita nějaké soustavy se dá velmi obecně vyjádřit jako \(\frac{ven}{dovnitř}\). Tedy:
$$\eta = \frac{W}{Q_1} = \frac{Q_1 – Q_2}{Q_1} = 1-\frac{Q_2}{Q_1}$$
A nyní si položmě otázku, kdy může být \(\eta\) rovno jedné — čili 100% účinnost. Buď bychom museli mít nekonečně velké teplo \(Q_1\), abychom minimalizovali zlomek jmenovatelem, anebo bychom museli mít absolutní nulu \(Q_2\), čímž bychom minimalizovali zlomek čitatelem. Druhého jmenovaného jsme přece jen blíže dosáhnout, ale přesto toho nejsme schopni dosáhnout absolutně.
Abychom si však popsali takový proces cyklicky, je potřeba použít tzv. Carnotova cyklu, což je teplený cyklus, kde někdy měníme stavy adiabaticky a někdy isotermicky. To opakujeme pořád dokola a sledujeme vstupy a výstupy, čímž jsme schopni opět spočítat efektivitu takové soustavy.
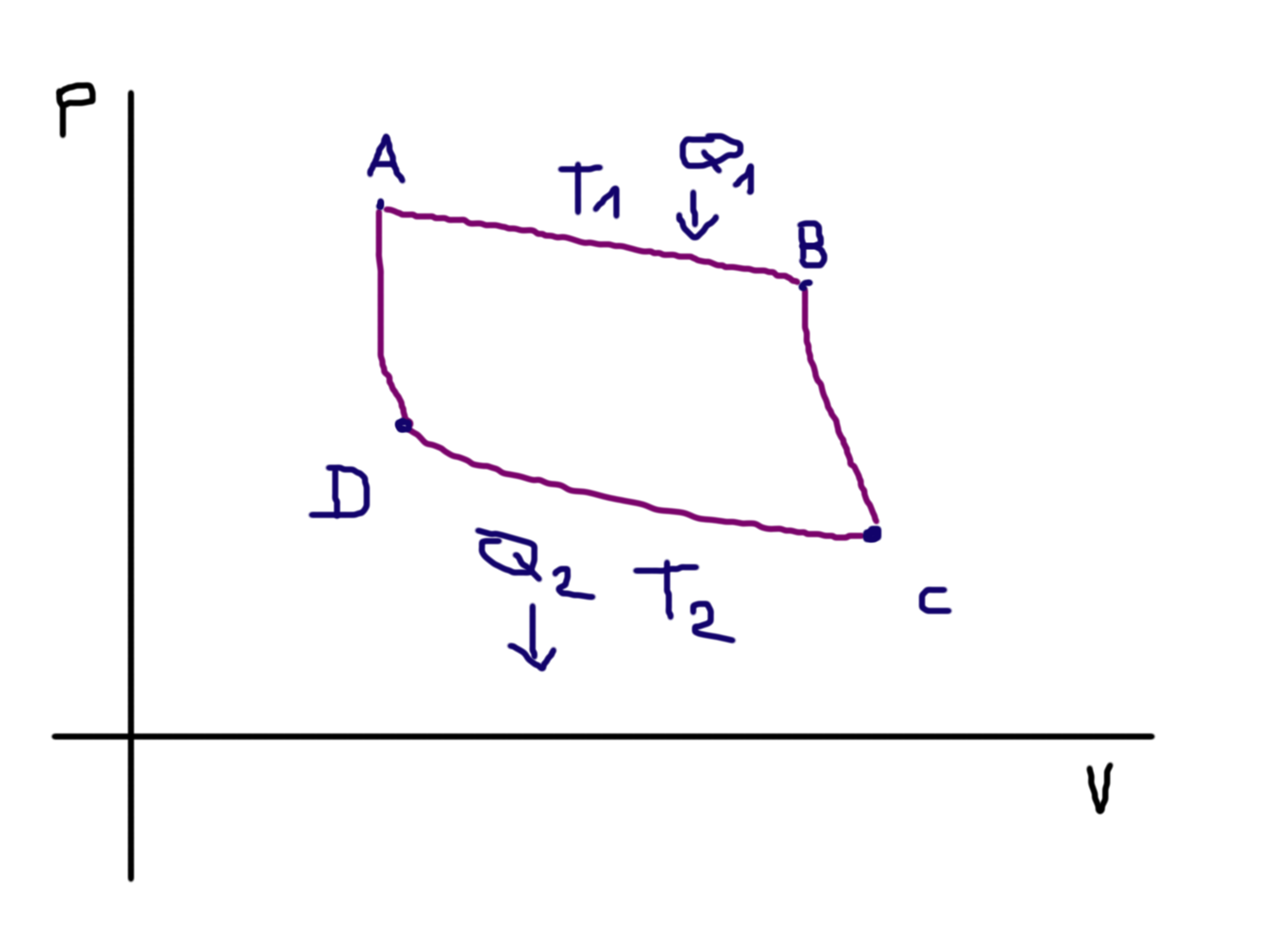
Představme si tedy znovu náš zelený píst ze začátku článku, kde se budeme snažit vyvolat adiabatické a isotermické změny. Abychom to však vzali trošku “profesionálně”, experimenty si necháme třeba do laboratoře, my si vše popíšeme krásně grafem, konkrétně tzv. PV grafem. Jak písmenka napovídají, \(P\) odpovídá tlaku a \(V\) odpovídá objemu:
Vynesme si nyní na ně několik bodů (samozřejmě postupně): Nejdříve začněme nějakým výchozím stavem, nazvěme si ho třeba \(A\):
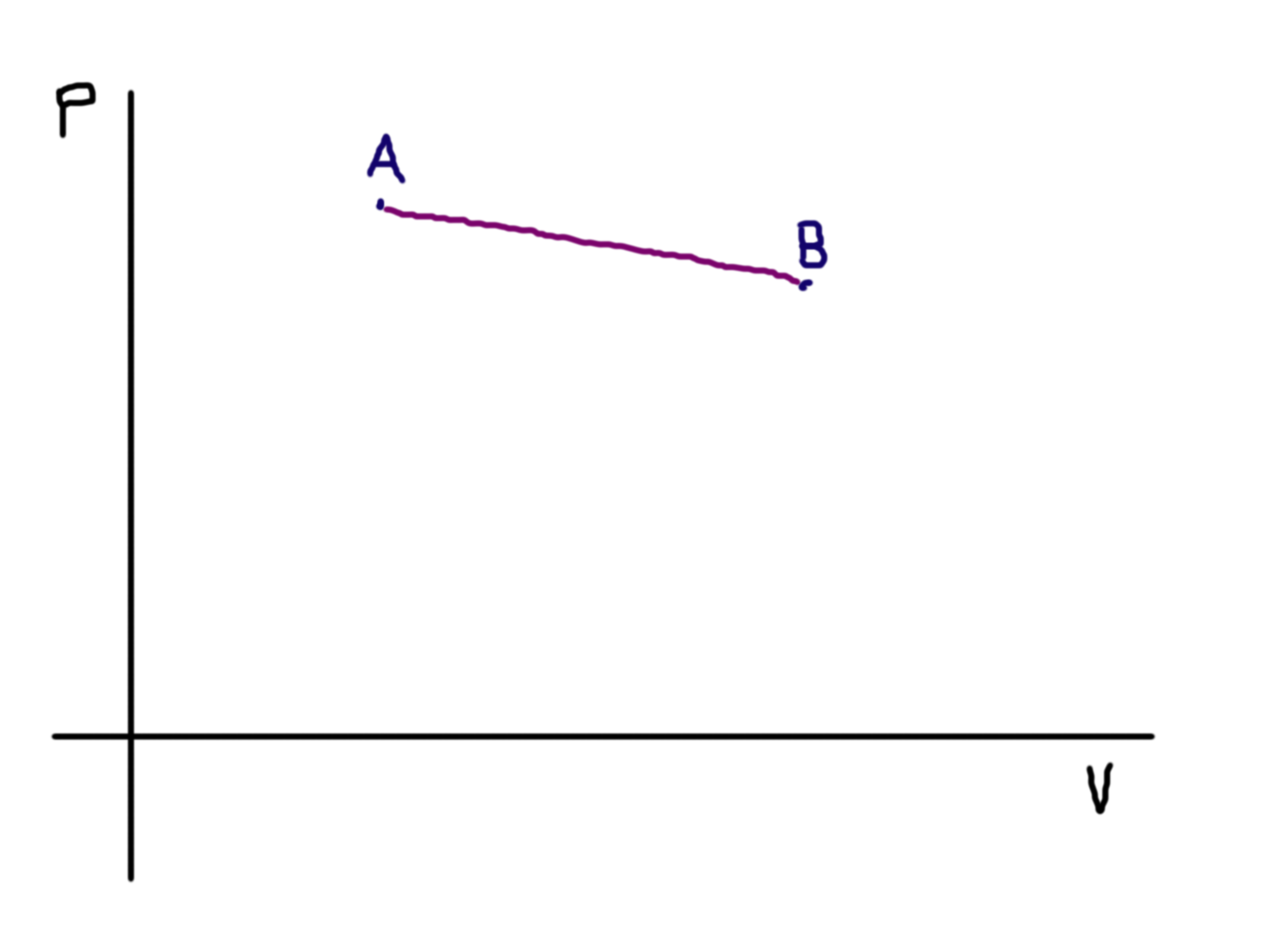
Od tohoto bodu se isotermicky budeme pohybovat k bodu B:
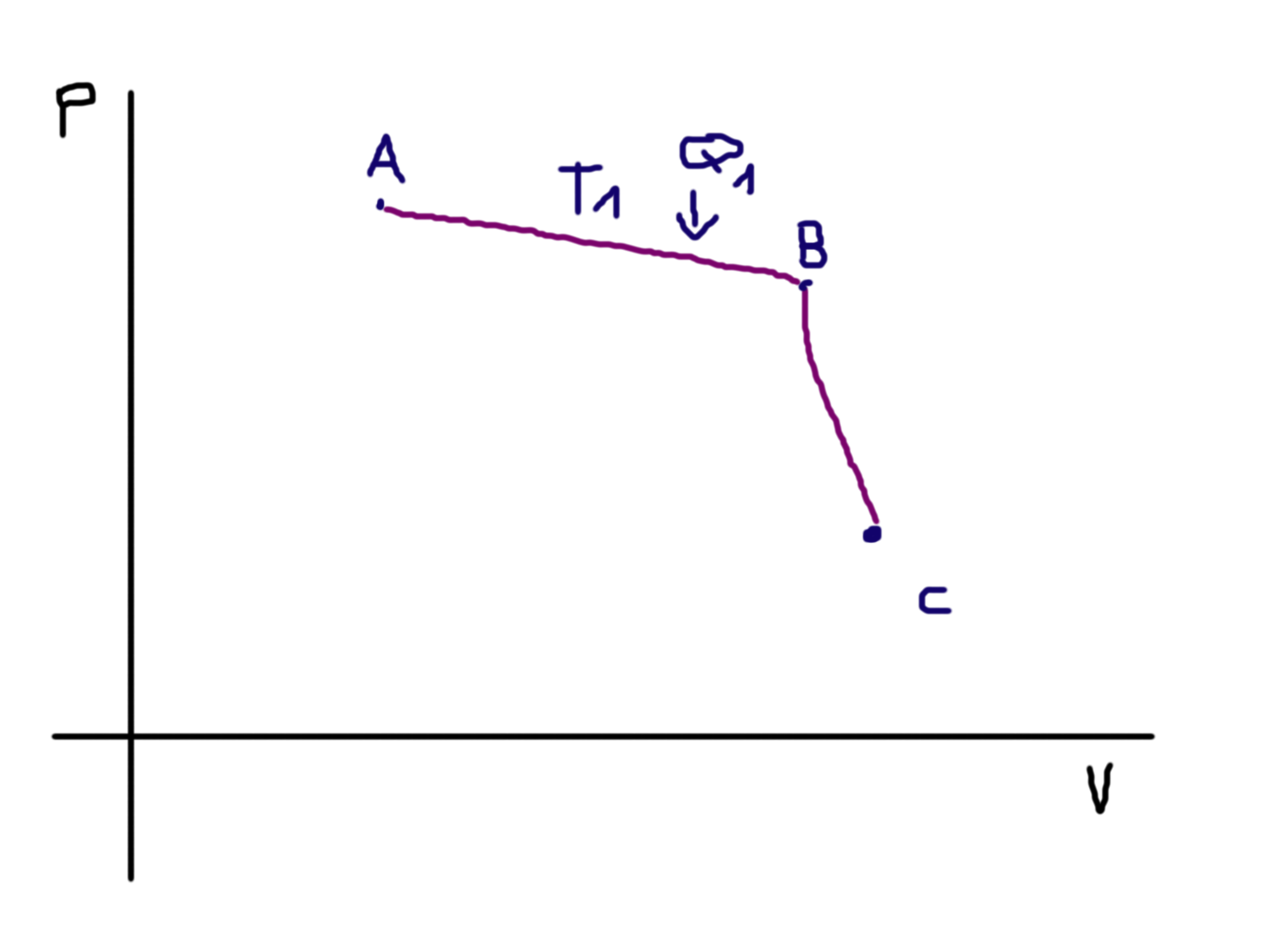
Během tohoto procesu vidíme, že se zvyšuje objem, avšak protože se jedná o isotermický děj, zůstává konstantní teplota, nazvěme ji \(T_1\). Musíme tedy do systému dodávat nějaké teplo, aby byla soustava vyrovnána, což také děláme. Dále přejděme k bodu \(C\), ke kterému se dostaneme adiabatickou cestou (žádné teplo dovnitř ani ven):
Protože se pohybujeme po adiabatě, žádné teplo nedodáváme ani nebereme, objem se příliš nemění, ale snižuje se tlak — konáme práci. V další iteraci se dostáváme do bodu \(D\) — opět jako isotermický děj:
No a protože platí totéž, co pro \(AB\) posun, tedy že se mění objem, ale teplota zůstává konstantní, musíme nějaké teplo odevzdávat, čili zde vidíme “vznik” \(Q_2\). Nakonec nám zbývá poslední adiabatický děj, totiž \(DA\)[18]A ne, není to Dragon Age! 🙂 :
Jsme tedy opět “na začátku” našeho cyklu a ten se pořád dokola opakuje. Vyjádříme-li si nyní z nám již velmi dobře známé rovnice ideálního plynu tlak, dostaneme:
$$ PV = nRT $$
$$ P = \frac{nRT}{V}$$
Dále víme, že \(\mathrm{d}u = \mathrm{d}q – P\mathrm{d}V\), jenže co vyjadřuje \(\mathrm{d}u\)? Vyjadřuje “změnu množství tepla” (či vnitřní energie systému). Když se však na cyklus podíváte, začali jsme v bodě \(A\), a ve stejném jsme vlastně i skončili. Nedodali jsme proto žádnou energii navíc, všechna byla vyzářena v podobě ztrát či tak podobně — můžeme tedy s klidným srdcem položit \(\mathrm{d}u = 0\) a potom už je snadné psát:
$$ 0 = \mathrm{d}q – P\mathrm{d}V$$
$$\mathrm{d}q = P\mathrm{d}V$$
Můžeme integrovat, pro každou teplotu musíme zvlášť:
$$ Q_1 = \int_{V_A}^{V_B} nRT_1 \frac{\mathrm{d}V}{V}=nRT_1\ln\frac{V_B}{V_A}$$
$$ Q_2 = – \int_{V_C}^{V_D} nRT_2 \frac{\mathrm{d}V}{V}=- nRT_2\ln\frac{V_D}{V_C}$$
Minus u \(Q_2\) značí, že teplo “dáváme ven”, tzn. ubývá (a proto mínus). Dříve jsme si vyjádřili, že \(\eta\), tedy účinnost systému, se dá zapsat jako:
$$ \eta = 1-\frac{Q2}{Q1}$$
A nezbývá, než dosadit nově zjištěná “kvé”:
$$ \eta = 1-\frac{nRT_2\ln\frac{V_C}{V_D}}{nRT_1\ln\frac{V_B}{V_A}} = 1 – \frac{T_2\ln\frac{V_C}{V_D}}{T_1\ln\frac{V_B}{V_A}}$$
Jak to zjednodušit? Dokažme, že část zlomku, kde porovnáváme logaritmy, je konstantní, konkrétně je rovna jedné.
Víme už, že:
$$ \frac{T_2}{T_1} = \left(\frac{V_1}{V_2}\right)^{\xi-1}$$
A po přeházení proměnných tedy:
$$T_2V_2^{\xi-1} = T_1V_1^{\xi-1}$$
Z grafu Carnotova cyklu můžeme dále určit, že pro dané objemy a tedy i krajní body vpravo a vlevo můžeme dát do rovnosti (tohle je trošku těžší krok na představivost, ale podívejte se pořádně na graf, vyplyne to z toho 🙂 ):
Pro body “vpravo”:
$$T_1V_B^{\xi-1} = T_2V_C^{\xi-1}$$
Pro body “vlevo”:
$$ T_1V_A^{\xi-1} = T_2V_D^{\xi-1}$$
Tuto soustavu tedy můžeme přepsat jako:
$$\frac{T_1V_B^{\xi-1}}{T_1V_A^{\xi-1}} = \frac{T_2V_C^{\xi-1}}{T_2V_D^{\xi-1}}$$
Můžeme pokrátit teploty a získáme:
$$\left(\frac{V_B}{V_A}\right)^{\xi-1} = \left(\frac{V_C}{V_D}\right)^{\xi-1}$$
A tedy vidíme, že obsahy závorek musí být stejné, aby rovnost platila. Vrátíme-li se proto k původnímu vzorci pro \(\eta\):
$$ \eta = 1-\frac{nRT_2\ln\frac{V_C}{V_D}}{nRT_1\ln\frac{V_B}{V_A}} = 1 – \frac{T_2\ln\frac{V_C}{V_D}}{T_1\ln\frac{V_B}{V_A}}$$
Vidíme, že můžeme s klidem poměr logaritmů pokrátit, protože se prostě jedná jedné. Zbyde nám tedy:
$$\eta = 1-\frac{Q_2}{Q_1} = 1-\frac{T_2}{T_1}$$
A z toho jasně plyne, že:
$$\frac{Q_2}{Q_1} = \frac{T_2}{T_1}$$
Trošku popřehazujeme písmenka, a získáme:
$$\frac{Q_2}{T_2} = \frac{Q_1}{T_1}$$
kde poměr \(\frac{Q}{T}\) je konstantní a nazveme ho (hurá potlesk) entropie. Tu dále budeme označovat jako \(S\).
Neklesavost entropie
Určitě jste někde (nedivil bych se, kdyby v nějakém sci-fi) slyšeli, že entropie vesmíru stále stoupá. Co si pod tím představit? Proč? Jak? Dokažme si nyní na našem malém experimentu s Carnotovým cyklem a tepelným strojem, co to znamená a kde se něco takového vzalo.
Výše jsme si vyjádřili dva vztahy:
$$ \eta_{max} = 1-\frac{T_2}{T_1}$$
a
$$ \eta_{max} = \frac{W}{Q_1}$$
Není nic lehčího, než je spojit přes \(\eta\) dohromady:
$$\frac{W}{Q_1}=1-\frac{T_2}{T_1}$$
a tedy:
$$ W \leq Q_1 \left(1-\frac{T_2}{T_1}\right)$$
Proč jsem přidal “nerovná se”? Přesně ze stejného důvodu, proč jsem k \(\eta\) přidal index “max” — jedná se totiž o výpočty s maximální účinností, nikoliv absolutní. Proto práce bude vždy maximálně taková, jaká je — případně může být jen nižší.
Dále víme, že \(W = Q_1 – Q_2\). Můžeme tedy psát:
$$ Q_1 – Q_2 \leq Q_1 \left(1-\frac{T_2}{T_1}\right)$$
Roznásobíme:
$$ Q_1 – Q_2 \leq Q_1-\frac{Q_1 T_2}{T_1}$$
a vidíme, že \(Q_1\) můžeme z rovnice s klidnou duší vyhodit:
$$- Q_2 \leq -\frac{Q_1 T_2}{T_1}$$
Otočíme:
$$ Q_2 \geq \frac{Q_1 T_2}{T_1}$$
Přeházíme písmenka:
$$ \frac{Q_2}{T_2} \geq \frac{Q_1}{T_1}$$
A to je vše 🙂 Vidíme, že po skončení procesu bude entropie vždy ne menší, tedy stejná či větší, než před začátkem takového procesu. A to je důvod, proč entropie neustále roste — protože prostě nemůže být menší.
To by pro začátek s termodynamikou stačilo, příště se zase podíváme na nějaké částice, tak se těšte 😉 Zde si též můžete stáhnout mé poznámky k článku, ze kterých jsem vycházel (pokud to po mně přečtete) 🙂
Poznámky pod čarou
| ⇧1 | Další informace kupříkladu na http://fyzika.jreichl.com/main.article/view/581-prvni-termodynamicky-zakon |
|---|---|
| ⇧2 | Zde by to chtělo podotknout, že mluvíme samozřejmě o fyzikální práci. Takže pokud jste nezaměstnaní a zhubnete, práci nedostanete 🙂 |
| ⇧3 | Proč ne tlaku? Tlak je totiž definován pomocí těchto dvou veličin (není to nezávislá veličina). Proto tedypouze teplota a objem. |
| ⇧4 | Více informací: http://scienceworld.wolfram.com/physics/Enthalpy.html |
| ⇧5 | dále jen TZ1 |
| ⇧6 | Nevím, jak to lépe přeložit, každopádně další informace o tom zde: http://en.wikipedia.org/wiki/Triple_product_rule. |
| ⇧7 | Tzn. jedná se o dokonalý stroj, který převádí tepelnou energii na energii pohybu pístu třeba — sice je to ideální zařízení, ale nám se to teď dost hodí. |
| ⇧8 | a již brzy se dostaneme ke slíbené entropii, slibuji 🙂 |
| ⇧9 | A samozřejmě až budete vědět, co to je a jak je definováno, můžete si to tam virtuálně přiřadit |
| ⇧10 | pozor, nokoliv teplota!! |
| ⇧11 | Jen přeházíme “sem a tam” přes rovnítko různé proměnné tak, aby nám na jedné straně u sebe zbyly diferenciály a proměnné teploty, na druhé objemu. |
| ⇧12 | molární množství látky |
| ⇧13 | Jak na to se dozvíte v tom slibovaném článku o integrálech, ale když se na to zakoukáte, vymyslíte to 🙂 |
| ⇧14 | Tuten paznak se čte jako “ksí” |
| ⇧15 | Informace např. zde: http://www-history.mcs.st-andrews.ac.uk/Biographies/Carnot_Sadi.html |
| ⇧16 | Moc hezké informace a interaktivní aplety mají třeba zde: http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/carnot.html |
| ⇧17 | Dnes nám to už může přijít jako samozřejmost, ale stejně po světě běhá spoustu lidí, co si myslí, že vynalezlo perpetum mobile, což jeho existenci přímo jako důsledek tohoto zjištění vyvrací. |
| ⇧18 | A ne, není to Dragon Age! 🙂 |











1 komentář u „Entropie a termodynamické zákony“
Komentáře nejsou povoleny.