Vítám vás u pokračování tématu o polarizaci a spinu částic. V prvním díle jsme zlehka naznačili matematický aparát a obecné principy, v tomto článku jich dále budeme využívat, proto pokud budete potřebovat, velmi doporučuji otevřít si první článek a v případě matematických nejasností zde se na něho odkazovat, mělo by tam být vysvětleno vše důležité.
Archiv štítku: derivace
Limity
Naprosto zákaldní matematickou znalostí jsou limity — ať už pro pochopení derivací či integrací, tak často i pro pochopení některých průběhů funkcí.
Zápis limity
Limita má specifický matematický zápis, naprosto obecně vypadá např. takto:
$$ \lim_{x\to L} f(x) $$
Tento zápis nám doslova říká “vezměte \(x\) a nastavujte mu tak velkou hodnotu, aby se co nejblíže přiblížila k hodnotě \(L\) a sledujte při tom, co funkce závislá na \(x\) dělá.”
Několik příkladů k úplnému pochopení:
$$ \lim_{x\to 0} x = 0$$
To je snad jasné — pokud budu \(x\) přibližovat nule, potom se… \(x\) bude přibližovat nule 🙂 Přitvrdíme…
$$ \lim_{x\to 0} 15x = 0$$
Zde samozřejmě platí totéž, co výše — i kdybych to násobil libovolným reálným číslem, pořád budu mít výsledek nulový. Prostřednictvím limit však můžeme zapisovat i výrazy, které bychom jinak v matematice nazvali jako “chybné” či “nedávající smysl”. Nula zapsaná “s plusem” znamená, že se k dotyčné nule postupně přibližuji zprava, tedy z kladnější části číselné osy — proto plus. U druhého znaménka to platí přesně opačně.
$$ \lim_{x\to0^+} \frac{1}{x} = \infty $$
$$ \lim_{x\to0^-} \frac{1}{x} = -\infty $$
U nevlastních limit[1]to jsou takové, které nemají “normální” výsledek můžeme takto tvrdit, že výsledek tzv. roste nade všechny meze. Podobně (přesně inverzně) to platí i u vlastních limit v nevlastním bodě:
$$ \lim_{x\to \infty} \frac{1}{x} = 0$$
Limitní aritmetika
Když teď už víme, jak fungují limity, můžeme se podívat na pár příkladů, které se v praxi často objevují. Začněme polynomem:
$$ \lim_{x\to \infty} \frac{2x^3 – 6x^2-145x + 17}{3x^3 – 2x^2 – 6} $$
Pokud bychom měli určovat třeba vlastnosti tohoto polynomu, budeme hledat kořeny rovnice v čitateli, kořeny rovnice ve jmenovateli, abychom omezili dělení nulou a podobně. Nicméně tady nás zajímá jediné — jak se bude daný výraz chovat, pokud \(x\) budeme zvětšovat až k nekonečnu.
Nyní však musíme udělat drobnou odbočku a ukázat si pár elementárních znalostí — např. jak se budou chovat různé poměry a zlomky limitně:
$$ \lim_{x\to \infty} \frac{1}{x} = 0$$
To už známe. Nicméně pokud zde bude takovýto poměr?
$$ \lim_{x\to \infty} \frac{x}{x} = ?$$
Víme, že dělit nulu nulou, stejně jako nekonečno nekonečněm (což je vlastně totéž, pokud mluvíme o limitách), je trošku nekošer, co se matematiky týče. Ale hleďte! Zde se řeší limity, zde nám věci, jako že bude mít polynom ve jmenovateli nulu, vlastně nevadí! Můžeme tedy dotyčný zlomek s klidným svědomím zkrátit a vyjde:
$$ \lim_{x\to \infty} \frac{x}{x} = \lim_{x\to \infty} \frac{1}{1} = 1$$
Vyřadili jsme tím “ze hry” tedy jakékoliv \(x\) a výsledek na něm vůbec nezávisí. A co třeba následující?
$$ \lim_{x\to \infty} \frac{x^n}{x^n} $$
Můžeme prostě pokrátit stejně, jako v případě výše, výsledek je tedy opět jednička. Případně můžeme rozložit na :
$$ \lim_{x\to \infty} \frac{x^n}{x^n} = \lim_{x\to \infty} \frac{x}{x} \frac{x^{n-1}}{x^{n-1}} $$
a takto to řešit do nekonečna 😉 S stejně tak logicky odvodíme, že:
$$ \lim_{x\to \infty} \frac{nx}{mx}$$
bude rovno \(\frac{n}{m}\) — protože “cokoliv” krát jedna je “cokoliv” 😉
Zkusme nyní další případ:
$$ \lim_{x\to \infty} \frac{x^2}{x} = ?$$
V matematice (ono i ve fyzice, ale v matematice obzvlášť) platí, že pokud neznáte řešení komplexního problému, dekomponujte ho na řadu “menších” problémů, které nezávisle řešit umíte. Což můžeme udělat i zde. Výše uvedené tedy můžeme přepsat jako součin:
$$\lim_{x\to \infty} \frac{x^2}{x} = \lim_{x\to \infty} x \frac{x}{x}$$
Druhý zlomek už řešit umíme, to víme, že je \(1\), takže:
$$ \lim_{x\to \infty} \frac{x^2}{x} = \lim_{x\to \infty} x = \infty$$
Vidíme tedy, že pokud je v čitateli vyšší mocnina než ve jmenovateli, zlomek vystřelí do nekonečných výšin. A co pokud je to opačně? Samozřejmě už správně tušíte:
$$ \lim_{x\to \infty} \frac{x}{x^2} = \lim_{x\to \infty} \frac{1}{x} \cdot \frac{x}{x} = \lim_{x\to \infty} \frac{1}{x} = 0$$
Je to prosté! 🙂 Vraťme se nyní tedy k našemu původnímu příkladu:
$$ \lim_{x\to \infty} \frac{2x^3 – 6x^2-145x + 17}{3x^3 – 2x^2 – 6} $$
A rozepišme si zlomek na 3 zlomky:
$$ \lim_{x\to \infty} \frac{2x^3 – 6x^2-145x + 17}{3x^3 – 2x^2 – 6} = $$
$$ = \lim_{x\to \infty} \frac{2x^3}{3x^3 – 2x^2 – 6} + \lim_{x\to \infty} \frac{ – 6x^2}{3x^3 – 2x^2 – 6} + \lim_{x\to \infty} \frac{-145x}{3x^3 – 2x^2 – 6} +\lim_{x\to \infty} \frac{17}{3x^3 – 2x^2 – 6} $$
Když se nyní podíváme na poslední tři limity, už vidíme, kam směřují — řekli jsme, že pokud je mocnina čitatele menší než jmenovatele, zlomek bude limitovat k nule. Můžeme tedy velmi snadno všechny tyto tři limity položit rovny nule a zbyde tak pouze zlomek se stejnou mocninou.
A co jsme si dále ukázali — že limita \(\frac{x^n}{x^n}\) je rovna jedné! Čili rovnou krásně vidíme, že výsledek limity bude \(\frac{2}{3}\).
Zajímavé poměry
U polynomu je tedy snad už jasné, nicméně pojďme se podívat na další “moc hezké” limity. Například tato:
$$ \lim_{x\to0} \frac{\sin(x)}{x}$$
Podíváme-li se na graf takové funkce, vidíme (chceme vidět), že limita bude rovná jedničce. Graficky tedy můžeme toto tvrdit, nicméně, jak to doopravdy spočítat?
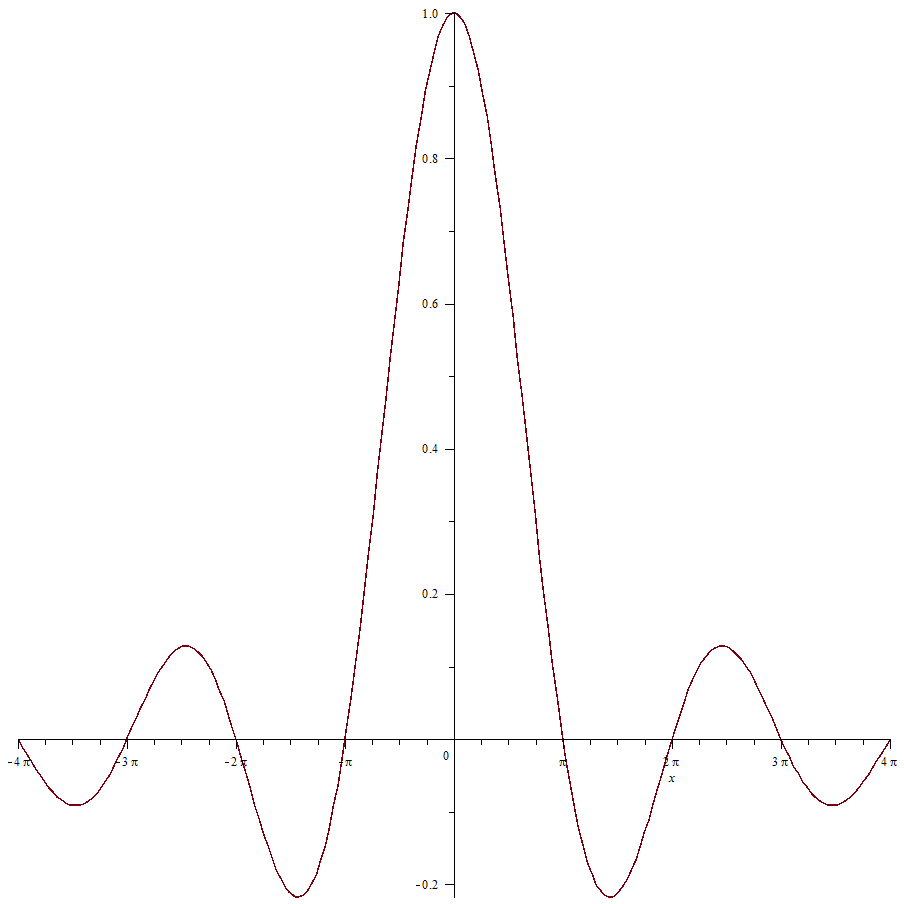
Na pomoc si vezmeme tzv. L’Hospitalovo pravidlo, tedy pravidlo, které říká následující:
$$ \lim_{x\to0}\frac{f_1(x)}{f_2(x)} = \lim_{x\to0}\frac{f_1^\prime(x)}{f_2^\prime(x)}$$
Tedy že limita poměru funkcí je limitou poměru derivací těchto funkcí. O derivacích si můžete přečíst v článku o kinematice, zde tedy použiji pouze rychlou derivaci:
$$ \lim_{x\to0}\frac{\sin(x)}{x} = \lim_{x\to0}\frac{\sin(x)^\prime}{x^\prime} = \lim_{x\to0}\frac{\cos(x)}{1}$$
A to už je snané — budeme-li do \(\cos(x)\) za \(x\) dosazovat nulu, bude se cosinus blížit k jedničce. Ve jmenovateli máme jedničku — výsledný poměr je tedy jednička 🙂
Poznámky pod čarou
| ⇧1 | to jsou takové, které nemají “normální” výsledek |
|---|
Entropie a termodynamické zákony
V článku o odvození rovnice ideálního plynu jsme nakousli několik termodynamických zákonitostí, nicméně bylo by dobré, abychom se na termodynamiku podívali i trochu obecněji a do hloubky.
Rovnici idálního plynu jsme si již odvodili, nyní však pro připomenutí: