Dostal jsem od instruktora v autoškole velmi zajímavý příklad — pokud ho znáte, tím lépe, ale fakt jsem ho neznal a hodně se mi líbil, zkusil jsem tedy přijít na nějaké řešení 😉 😉 Nakonec mi z toho “vypadlo” něco normálního (tedy reálného), svůj postup tedy uveřejňuji zde.
Mějme následující zadání: Existuje studna neznámé hloubky a průměru, do které hodíme dva klacky; jeden třímetrový, druhý dvoumetrový. Předpokládejme, že jsou “v rovině” a jejich místo setkání je nad dnem studny ve výšce 1 metr. Otázka zní — jaký je průměr takové studny.
Situační obrázek bych navrhl asi takto:
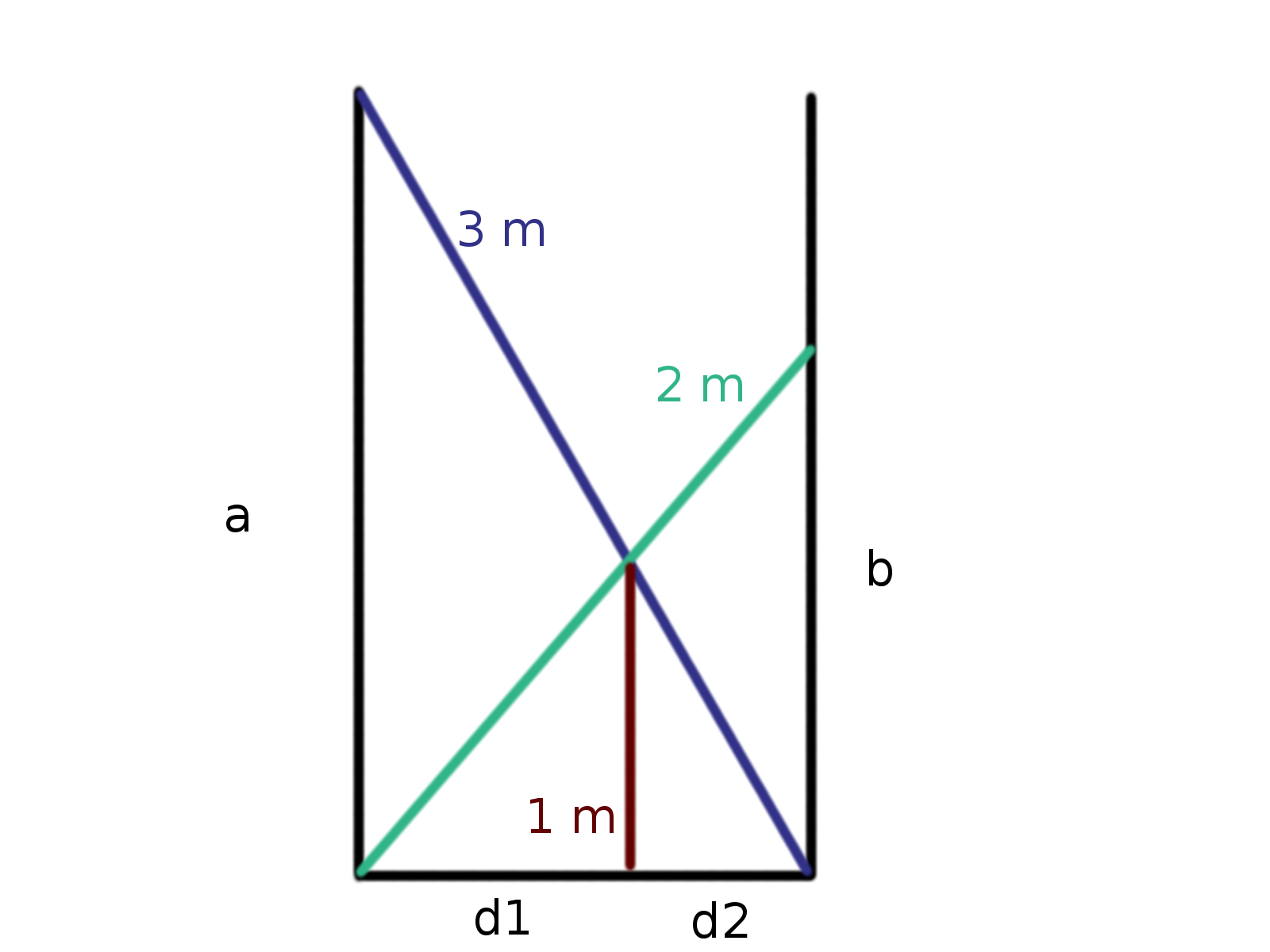
Začal bych asi svojí první myšlenkou, a to sice že řešení se určitě bude dělat nějak přes podobnosti trojúhelníků. Začal jsem tedy zuřivě hledat různé podobnosti, některé mě zavedly do slepých cest (tedy ne, že by si některé trojúhelníky nebyly podobné, ale bylo mi to k ničemu), ale nakonec se jedna cesta zadařila, tu zde i prezentuji 🙂
Ze všeho nejdříve si napíšeme rovnice, ze kterých budeme vycházet. Jedné se o soustavu různě propletených pravoúhlých trojúhelníků. Ze všeho nejdříve si určeme, že celkový průměr \(d\) bude samozřejmě roven:
$$d = d_1+d_2$$
A nyní můžeme pracovat s jednotlivými stranami:
$$\begin{array} aa^2+d^2 & = & 3^2 \\ b^2 + d^2 & = & 2^2\end{array}$$
Tím jsme popsali dva hlavní (velké) trojúhelníky. Nyní popíšeme vztahy v trojúhelníku s naznačenou výškou. Vyjdeme právě z té podobnosti, tedy že:
$$\frac{d_1}{v} = \frac{d}{b}$$
tedy po dosazení \(v=1\) získáme:
$$d_1 = \frac{d}{b}$$
a obdobně
$$d_2 = \frac{d}{a}$$
Vyjádříme si jednu a druhou stranu:
$$d_1=\frac{d}{b}, d_2=\frac{d}{a}$$
a dosadíme do výše uvedené rovnice součtu částí průměru:
$$d=\frac{d}{b}+\frac{d}{a}$$
Z toho vyjádříme jednu či druhou proměnnou, začněme třeba \(a\):
$$\frac{d}{a}=d-\frac{d}{b}=\frac{db-d}{b}$$
z toho tedy:
$$a = \frac{b}{b-1}$$
případně
$$b = \frac{a}{a-1}$$
Toto dosaďme do úplně prvních dvou rovnic pro velké trojúhelníky:
$$d^2+\frac{b^2}{\left(b-1\right)^2}=3^2$$
$$d^2+b^2=2^2$$
Vyjádříme si z druhé rovnice \(d^2\) a dosadíme do první:
$$2^2-b^2+\frac{b^2}{\left(b-1\right)^2}=3^2$$
Převedeme na rozumný tvar a vyřešíme jako rovnici 4. řádu, třeba pomocí Wolframu, to už je jedno (ale můžete zkusit ručně) a vyjdou 4 řešení, z toho 2 komplexní, která rovnou zavrhneme.
$$b_1=0,7009 ; b_2=1,5761$$
Které vybrat? To zatím nevíme, každopádně pokud dosadíme do rovnice pro průměr a odmocníme, vyjdou nám (prozatím) dvě řešení:
$$d_{I}=\sqrt{2^2-b_1^2} = 1,23$$
$$d_{II}=\sqrt{2^2-b_2^2} = 1,87316$$
Musíme vyjádřit tedy stejné rovnice, akorát pro vyjádřené \(b\), tedy:
$$b=\frac{a}{a-1}$$
Stejným postupem jako výše dostaneme rovnici:
$$3^2-a^2+\frac{a^2}{\left(a-1\right)^2}=2^2$$
a ta po vyřešení dá dva reálné kořeny:
$$ a_1=-2,34$$
$$a_2 = 2,7357$$
První rovnou vyhodíme, délky prostě záporné nechceme, držme se toho 🙂 Dosadíme tedy \(a_2\) a vyjde:
$$d=\sqrt{3^2-a_2^2}=1,2312$$
To se tedy shoduje s řešením “z druhé strany” problému — proto tento výsledek prohlásíme za finální. Průměr studny je tedy \(1,23\) metrů.