Tento článek nedávám ani do doplňkových článků, protože s fyzikou má společného fakt jen minimálně. Rovnou ho tedy dávám do “zábavy”. Nicméně pokud vám tato čísla nic neříkají, nejspíše patříte k té šťastné množině lidí, které průnik s množinou lidí, kteří věří či propagují tento nesmysl, je množina prázdná[1]Prostě jste o tom neslyšeli 🙂 .
O co se tedy jedná? Zastánci této podivné hypotézy říkají, že hudba je při podladění o 8 Hz příznivější tělu a mysli, než pokud se hraje v klasickém ladění. Možná by to však chtělo trošku alespoň fyzikálně zmínit, jak je to vlastně s laděním (když už se tedy máme bavit o fyzice).
Tóny
Asi to každý znáte — tón, zvuk, hluk; tyto termíny se definují snad už na ZŠ, čili nebudu je dlouho rozebírat, jen stručně: tón je na rozdíl od hluku homogenní a periodický, zvuk je množina všeho, do čeho patří i tón, hluk atp.
Jak víte, zvuk je mechanické vlnění nějakého prostředí, v našem případě vzduchu, které tímto přenáší nějakou zvukovou informaci. Tu pak mozek přes periferie (ucho) zpracovává na hudební či zvukový vjem.
Během historie se chápání “hudby” jako soustavy tónů poměrně dost bouřlivě vyvíjelo, nicméně to, že dnes používáme klasické tóniny, na které jsme zvyklí, není jen tak náhodou. Historii přenechám historikům, popíšeme si všechno pěkně fyzikálně.
Základní tón, harmonická, intervaly
Pokud vás zajímá více z hudební teorie, přečtěte si články, kde tyto věci popisuji (či případně články o itervalech) z hudebního hlediska, nicméně nyní pouze fyzikálně:
Jak jsme již řekli, tón je generován nějakým vlněním, v našem případě se omezíme na harmonické vlnění:
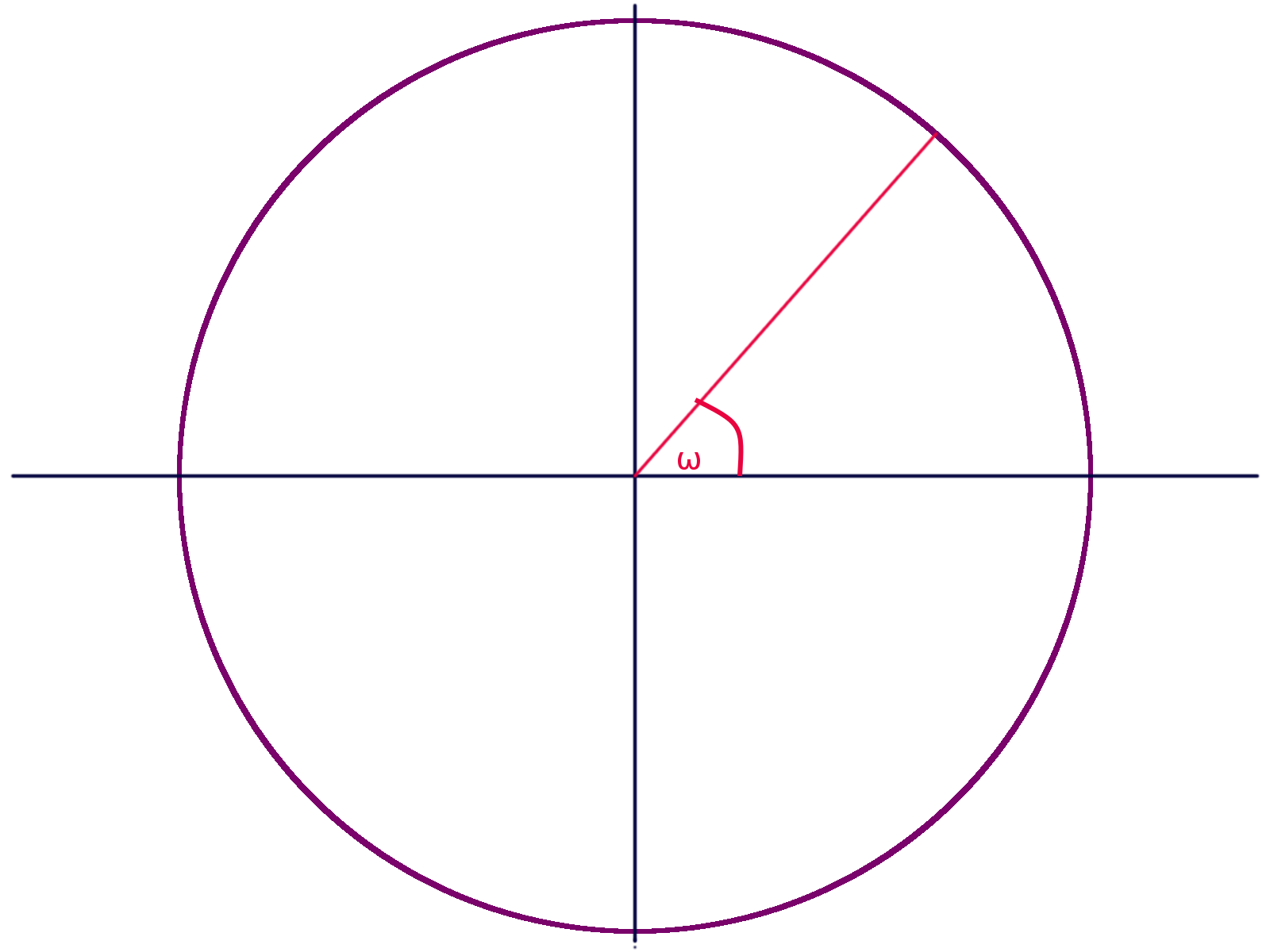
$$ f(t) = y = \sin \left(\omega t + \phi \right) $$
Kde \(y\) je aktuální výchylka, \(\omega\) je úhlová frekvence, \(t\) je čas, který do rovnice vstupuje jako parametr a \(\phi\) je fázový posuv. Nicméně pokud bychom si vytvořili např. takovýto tón, který má frekvenci 440 Hz, zněl by poněkud fádně, nezajímavě, nudně:
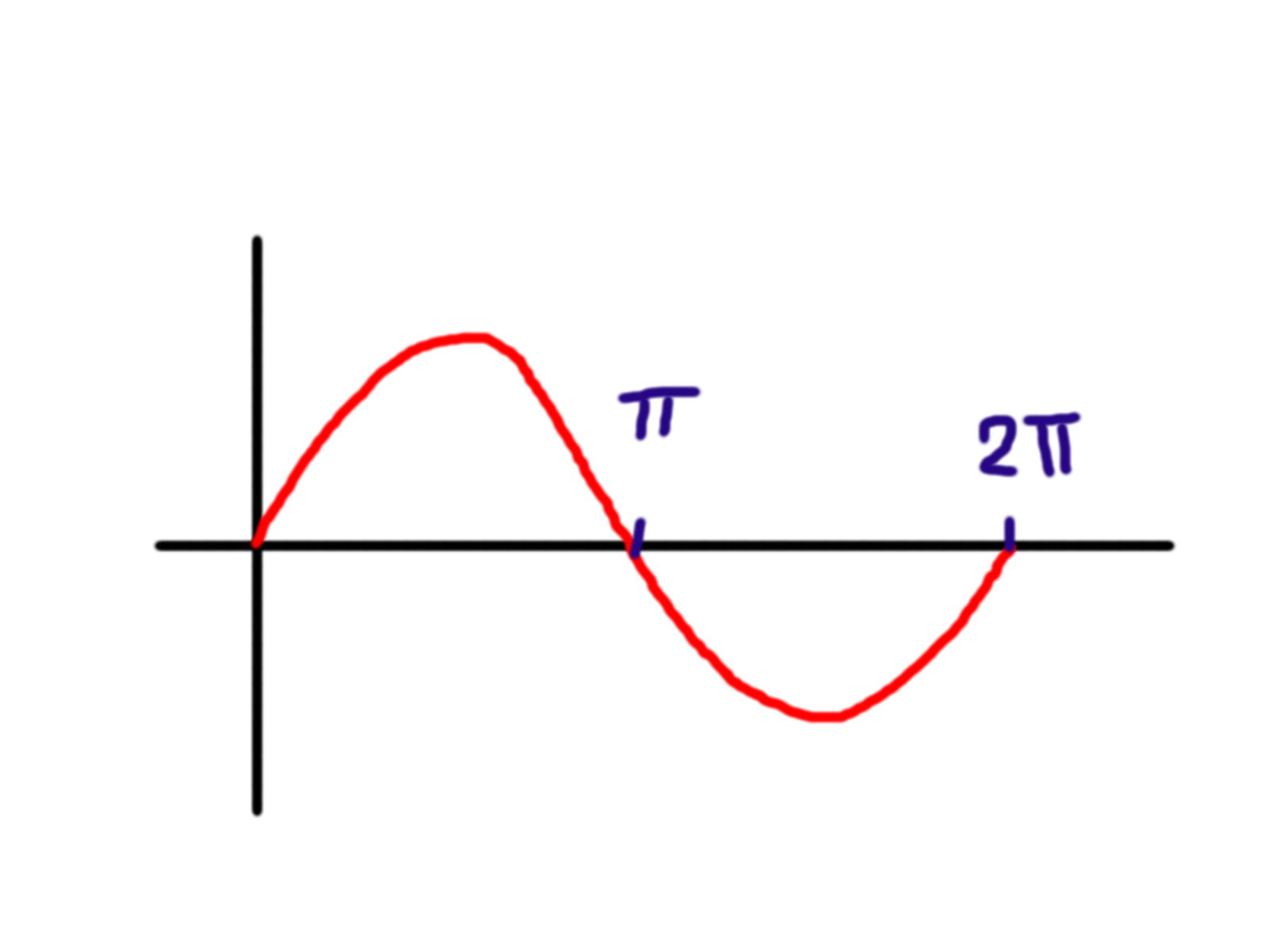
Krom toho, že tón není ani tak hlasitý a přesto je dost nepříjemný. Aby tón zněl lépe, je zapotřebí smíchat více tónů, nicméně ne jen tak ledabyle a náhodně, je potřeba je smíchat podle nějakých pravidel. Nejjednodušším mícháním je stav, kdy míchám různé “harmonické” frekvence. Co to je harmonická? Zde uvedený tón si můžeme zakreslit např. takto:

Jak vidíte, křivka se neustále opakuje — což je přesně to, co slovo “harmonická” znamená, je totiž periodická (tzn. neustále se opakující). Abychom mohli přidat třeba “druhou harmonickou”, musíme přidat takovou “harmonickou”, která bude mít stejné místo opakování — tedy aby tam, kde se křivka v nule[2]či tam, kam nás fáze posune potkává s osou \(t\), aby se i tam potkávala křivka další harmonické frekvence. Pokud přidáme např. frekvenci 880 Hz, tedy:

Výsledná frekvence bude prostým součtem těchto dvou křivek, tedy:
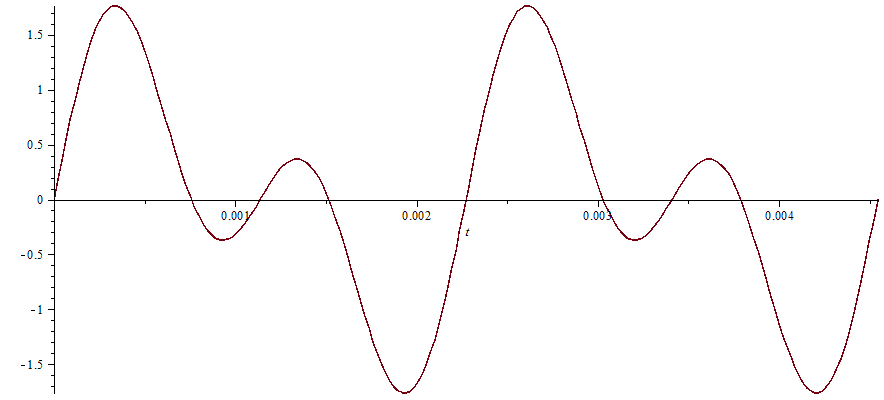
Sice už to není “sinusovka”, ale vidíme, že je to funkce neustále periodická. Zní nějak takto:
Kontrolní otázka (o další Fidorku!), pokud si tuten souzvuk pustíte, jak vysvětlíte ono “vlnění” zvuku? Proč zvuk nezní stále stejně, ale jako by pulzoval?
Nicméně tímto způsobem můžete přidat hromadu křivek, přidám ještě 220 a 110 Hz:

Vidíme, že křivka začíná být opravdu složitá, ale pořád je periodická, pořád se opakuje. Zní takto:
Nicméně když tento tón slyšíme, pořád je to prostě “takové jalové”. Jak se dosáhne toho, že tóny zní tak nějak lépe?
Zatím jsme totiž míchali pouze násobky harmonické — dvojnásobnou frekvenci, poloviční, čtvrtinovou. Tomuto intervalu mezi tóny se říká oktáva a vyjadřuje přesně to, co jsme si ukázali — dvojnásobek (či půlnásobek) původní frekvence. Pokud tón o frekvenci 440 Hz označíme jako \(a_1\), potom ten o frekvenci 880 Hz bude \(a_2\), frekvence 220 Hz odpovídá \(a\) a 110 potom \(A\) (čteme jako “á malé” a “á velké”).
To je však pořád jen tón A, ale kdo někdy viděl kytaru nebo klavír dobře ví, že je tam poněkud více tónů. Takže jak vzniknou? Začněme s další pěknou matematickou závislostí — čistou kvintou. Že je to kvinta, na to lidé přišli až později, nicméně kvinta má trojkové násobky. Smíchejme proto Náš tón 440 Hz s frekvencí 660 Hz, tedy \(\frac{3}{2}\) z 440 Hz:

Pro další intervaly platí další zákonitosti, nicméně takovýmto různým dělením dostaneme hromadu tónů, které když uspořádáme do našich známých stupnic, dostaneme tzv. Pythagorejské ladění, které tedy vznikne tím, že postupně přidáváme různé kvinty a posouváme je různě o oktávy nahoru a dolů. Nicméně dnešní nástroje nejsou laděny v Pythagorejském ladění, ale tzv. temperovaném, případně koncertním ladění.
Rozdíl mezi těmito laděními je mírně nad rámec fyzikálního článku, každopádně ve stručnosti — lidé si všimli, že pokud mírně posunou některé tóny, klavír bude třeba neustále “trochu rozladěn”, ale zase budou všechny tóny (současně hluboké a vysoké) k sobě ladit lépe. A právě takovému ladění se říká temeprované.
V článku o Fourierově analýze se můžete případně dočíst, jak je to se skládáním prakticky nekonečně mnoha různých frekvencí.
Zpět však k zastáncům “432 hypotézy”. Ti tvrdí, že pokud jako výchozí tón (tzn. vše ostatní je stejné) nepoužiji tón o frekvenci 440 Hz, ale 432 Hz, bude hudba příjemnější (s tím se dá i nedá souhlasit, záleží na skladbě), ale především že bude mít “pozitivní účinky na zdraví jedince”[3]Spíše tedy že “nebude mít negativní” účinky….
S argumenty této čtyři sta třicet dvojkové skupiny se dá poměrně slušně nesouhlasit; už jsem četl různé — od toho, že Mozart či Beethoven používali jiné ladění[4]Aby ne, když to bylo před staletími a moderní ladění se normalizovalo až kolem roku 1940., případně postují různé “pestrobarevné” obrázky s jakožemeditativní tématikou a vzájemně se poplácávají po zádech, jak to všem “čtyři sta čtyřicátníkům” nandali.
Názor si udělejte sami, případně zagooglete, že je to hloupost zjistíte po několika pročtených příspěvcích a studiích, nicméně nyní jen pro srovnání — stejný kousek písničky ve 440Hz ladění (tzn. beze změny) a ten samý kousíček se sníženým laděním (bohužel kvůli autorskému zákonu nemůžu více než 30vteřinovou ukázku):
Původní 440Hz verze:
“Vylepšená” 432Hz verze:
Jak slyšíme, “nějaký” rozdíl tam je. Nicméně vliv těchto změn je podle mého dost sporný. Často též vidíme různé obrázky, které tato skupina lidí posílá:

Je to sice krásné, ale netuším, proč by měla změna frekvence či toho, kde se různé harmonické potkávají, nějak ovlivňovat zdraví. Každopádně k výše uvedenému obrázku ještě pár slov:
Musíme totiž “probrat” ještě jeden typ vlnění, tzv. stojaté vlnění. To je narozdíl od postupného vlnění uvedeno “na místě”. Např. pokud klepnete do struny, ta se rozezní a bude “se vlnit” — stojaté vlnění. Vlna nikam necestuje, vlnové délky odpovídají různým poměrům délky struny. Postupné vlnění je takové, které pozorovatel vnímá jako vlnění až s tím, jak se věc, která se vlní, pohybuje — např. takový zvuk ve vzduchu. Vlny postupně jako kola po hození kamínku do vody cestují směrem od zdroje zvuku a pokud “narazí” na posluchače, ten je uslyší.
Nicméně stojaté vlnění má pár docela zajímavých vlastností — hráči na kytaru třeba ví, že pokud drknou na strunu tzv. flažolet tak, že ji rozezní jen “na půlce”, poté se druhá polovina struny rozezní též, akorát v opačné fázi 😉 Výsledná frekvence tónu bude tedy dvojnásobná, bude tedy o oktávu výše. Ale pokud si zkusíte takto rozeznít strunu třeba jen “o centimetr” vedle, už se tón neozve a vlnění okamžitě ustane.
Pokud bychom nakreslili obrázek toho, jak moc dobře struna zní, pokud v nějakém místě stiskneme strunu, dostaneme diagram, který je velmi podobný právě výše uvedným obrázkům (akorát ty berou osy jak X tak Y, v mém uvedeném případě se strunou by se aplikovala pouze osa X). Obrázky totiž zohledňují vliv prostředí, které celé kmitá — např. pokud jste v malé místnosti bez koberců, určitě slyšíte, že se zvuk tak podivně “nese” a rezonuje. A to přesně souvisí právě se stojatým vlněním — v některých frekvencích se vlny prostě nevyruší a budou znít déle a intenzivněji než v jiných.
Nicméně tato frekvence je naprosto závislá na rozměrech a tvaru místnosti. A stejně tak i výše uvedené obrázky, které mají simulovat vlnění na hladině vody — záleží kromě vstupní frekvence i na rozměrech misky či předmětu, který se vlní a kde toto vlnění zkoumáme.
Kdyby měli lidé své hlavy všechny stejně velké (tedy všichni lidé kdyby měli stejně velkou hlavu), samozřejmě by něco takového mohlo být zajímavé zkoumat. Bohudík tomu tak však není a každý si tak můžeme užívat jiného “vlnění”, které je nám příjemné.
Ohledně vlivu zvuku a frekvencí na tělo v biologickém slova smyslu opět požádám kolegu Lukáše, který se k tématu doufám též někdy vyjádří! 🙂