V minulém článku o Entropii a termodynamice jsem vám slíbil, že se zase vrátíme zpět k “nějakým částicím”. Nevrátíme se však k nějakým konkrétním, vrátíme se totiž pouze k jedné z jejich vlastností — spinu.
Ohledně spinu existuje takový problém — on se (jako vlastnost) dá jen velmi těžko představit. Můžu samozřejmě používat různých analogií, ale jak si ukážeme, když se trošku ponoříme do problematiky, dost těchto analogií (buďme upřímní — všechny) ukážou dříve či později nějaký zásadní smrtelný problém. Jak už je však zvykem, než se dáme do samých popisů spinů částic a jak s nimi fungovat, musíme si připravit lehké matematické podhoubí, abychom pochopili zákonitosti[1]Protože pokud chceme pochopit spin, musíme pochopit i ten zbytek..
Matematické základy
Budeme hojně využívat matic, vektorů a komplexních čísel. Bližší popis vektorových a maticových základních operací je mimo rozsah článku, v případě, že byste nevěděli “která bije”, o matematických operacích s vektory a maticemi doporučím některý z článků či prezentací volně ležících na internetu:
Primární studium — tedy zjistit jak co funguje:
- http://www2.ef.jcu.cz/~klufova/vyukaMAT2011_12/ZS/pred1_ZS.pdf
- http://www.mathsisfun.com/algebra/vectors.html [EN]
- https://www.khanacademy.org/math/precalculus/vectors-precalc [EN]
- http://www.onlinemathlearning.com/vectors-explained.html [EN]
Další materiály (sekundární studium):
- http://user.mendelu.cz/hasil/Data/CZ/Teach/Prez/01-VektMat.pdf
- https://vscht.cz/mat/El_pom/sbirka/Kapitola9.pdf
Bohužel je pro pochopení článku bezpodnínečně nutné, abyste alespoň zákaldní operace s vektory znali. Není potřeba žádných “hlubokých” znalostí, ale vysvětlovat co je to vektor či matice je bohužel mimo rozsah tohoto článku.
Nyní tedy jen stručně — jedna ze zákaldních operací, kterou budeme potřebovat, je maticový součin:
$$ \begin{pmatrix}a & b\end{pmatrix} \begin{pmatrix}c\\d\end{pmatrix}=a\cdot c + b \cdot d$$
$$\begin{pmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{pmatrix} \begin{pmatrix}b_1 \\ b_2\end{pmatrix} = \begin{pmatrix}a_{11}b_1 + a_{12}b_2 \\ a_{21}b_1 + a_{22}b_2\end{pmatrix}$$
Ohledně komplexních čísel budeme muset znát pojem komplexně sdružené číslo, což je takové číslo, jehož imaginární složka je převrácená. Označujeme “hvězdičkou”:
$$ X = a + \mathrm{i}b$$
$$ X^{*} = a – \mathrm{i}b$$
Diracova notace, systém bra-ket
Nyní, když víme, co budeme potřebovat jako teoretický základ, můžeme se s chutí vrhnout na to, co slibuje samotný podnadpis, tedy na tzv. Diracovo[2]či Diracovou, ale to se mi dost příčí notaci, nebo-li systém bra-ket.
Jak jste si zajisté všimli, slovo “bra” a “ket” dohromady v angličtině dají slovo “bra/c/ket” — tedy “závorky” 🙂 Velmi roztomilé. Každopádně systém je tvořen dvěma vektory:
Vektor bra (ano, podprsenka…), který vypadá následovně:
$$\langle{}a | = \begin{pmatrix}a_1 & a_2\end{pmatrix}^*$$
Tedy jedná se o řádkový vektor, kde jsou čísla navíc komplexně sdružená. U reálných hodnot toto samozřejmě nemá vliv (pokud komplexně sdružíte reálné číslo, získáte to samé reálné číslo), nicméně v případě s výpočty v komplexní rovině na to nesmíte zapomenout.
Vektor ket vypadá takto:
$$ |a\rangle = \begin{pmatrix}a_1 \\ a_2\end{pmatrix}$$
Samozřejmě bych mohl zobecnit do \(n\) dimenzí, ale pro zjednodušení teď uvažujme pouze dvě. S více dimenzemi se setkáme později, až se toto budeme snažit prakticky ukázat na polarizaci fotonu a elektronu.
S těmito vektory můžete provádět veškeré operace, na které jste zvyklí od běžných vektorů — např. součet dvou ket vektorů:
$$|a\rangle +|b\rangle= \begin{pmatrix}a_1 \\ a_2\end{pmatrix} + \begin{pmatrix}b_1 \\ b_2\end{pmatrix} = \begin{pmatrix}a_1+b_1\\a_2+b_2\end{pmatrix}$$
Co je pro nás však důležité (z hlediska fyziky), pokud vynásobíme bra vektor vektorem ket. Tedy:
$$\langle{}a|b\rangle$$
Toto můžeme pojmenovat jako skalární součin[3]Pro potřeby tohoto článku budu označovat takto, nicméně skalární součin normálně funguje bez komplexně sdružených čísel, takže toto ve své podstatě není “až tak” běžný skalární součin. Správně bych měl třeba nazývat konjugovaný sk. součin, ale jsem moc líný to psát takto dlouhé — proto odteď budu psát pouze “skalární součin”. Děkuji za pochopení. a velmi dobře ho známe z běžných výpočtů s vektory[4]Pro další informace doporučuji bezvadný zdroj všech možných matematických informací — web MatFyzu :-): http://wiki.matfyz.cz/index.php?title=16._Formalizmus_kvantov%C3%A9_teorie.
Můžeme tedy psát (pro dvourozměrný prostor):
$$\langle{}a|b\rangle = \begin{pmatrix} a_1^* & a_2^* \end{pmatrix} \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} = a_1^*b_1+a_2^*b_2$$
Výsledkem je tedy číslo, nikoliv vektor. Zkusíme-li nyní udělt komplexně sdruženou variantu toho součinu:
$$\langle{}a|b\rangle^* = a_1b_1^* + a_2b_2^*$$
Nyní už asi vidíme, že pokud bych otočil vektory:
$$\langle{}b|a\rangle = a_1b_1^* + a_2b_2^*$$
dostaneme totéž. Můžeme tedy s klidným svědomím psát:
$$\langle{}a|b\rangle = \langle{}b|a\rangle^*$$
Než budeme pokračovat dále, musíme se lehce zaměřit na matice a operace nad nimi. Pro ilustraci použiji 3×3 matice, ale samozřejmě bude fungovat v libovolných dimenzích. Začněme tedy popisem matice — jak jistě víte, matice má hlavní diagonálu:
$$A_{ij} = \begin{pmatrix}a_{11} & … & … \\ … & a_{22} & … \\ … & … & a_{33}\end{pmatrix}$$
A můžeme z matice udělat matici transponovanou, jednoduše to znamená, že přehodíme (zrcadlově) podle osy hlavní diagonály hodnoty. Jinými slovy přehodíme řádky a sloupce. Značíme indexem \(T\):
$$\begin{pmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{pmatrix}^T = \begin{pmatrix} a_{11} & a_{21} \\ a_{12} & a_{22}\end{pmatrix}$$
Samozřejmě platí, že transponujeme-li dvakrát za sebou stejnou matici, získáme zpět tu první.
Dále je snad samozřejmé, že pokud budeme chtít komplexně sdružené hodnoty z matice, musíme udělat všechny komplexně sdružené hodnoty všech prvků:
$$\begin{pmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{pmatrix}^* = \begin{pmatrix}a_{11}^* & a_{12}^* \\ a_{21}^* & a_{22}^*\end{pmatrix}$$
Samozřejmě můžeme výše uvedené dvě matice “zkombinovat” — tedy transponovat a ještě převést na komplexně sdružené hodnoty. Takovou matici značíme “křížkem” (v angličtině dagger — čili dýka):
$$\begin{pmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{pmatrix}^\dagger = \begin{pmatrix} a_{11}^* & a_{21}^* \\ a_{12}^* & a_{22}^*\end{pmatrix}$$
Nyní prozkoumejme, co se stane, pokud použijeme např. následující matici:
$$\begin{pmatrix}1 & 2+i3 \\ 2-i3 & 4\end{pmatrix}^\dagger$$
Pokud uděláme “křížkovanou matici”, zjistíme, že se bude rovnat sama sobě, tedy:
$$\begin{pmatrix}1 & 2+i3 \\ 2-i3 & 4\end{pmatrix}^\dagger = \begin{pmatrix}1 & 2+i3 \\ 2-i3 & 4\end{pmatrix}$$
Pokud něco takového nastane, můžeme o naší matici tvrdit, že je hermitovská.
Zkusme nyní, co se stane, zkusíme-li vynásobit matici a ket vektor:
$$A|b\rangle=\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\end{pmatrix} \begin{pmatrix} v_1 \\ v_2\end{pmatrix}$$
a dostaneme:
$$A|b\rangle=\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\end{pmatrix} \begin{pmatrix} v_1 \\ v_2\end{pmatrix} = \begin{pmatrix} a_{11}v_1 + a_{12}v_2 \\ a_{21}v_1 + a_{22}v_2 \end{pmatrix}$$
Abychom tady pořád jen nepísmenkovali, zkusme si to ukázat prakticky na příkladu:
$$\begin{pmatrix}1 & 1+i \\ 1-i & 2 \end{pmatrix} \begin{pmatrix}1 \\ 0 \end{pmatrix} = \begin{pmatrix}1 \cdot 1 + (1+i) \cdot 0 \\ (1-i) \cdot 1 + 2 \cdot 0\end{pmatrix} = \begin{pmatrix}1\\ 1-i\end{pmatrix}$$
Zpátky k fyzice
Po krátké cestě do útrob matematiky se opět můžeme vrátit k fyzice a k tomu, k čemu všechny tyto matematické věci využijeme. Po cestě samozřejmě přidáme ještě nějaké další, ale výše uvedené jsou takovou “matematickou startovací čárou” pro pochopení věcí dalších.
Budeme se bavit o polarizaci částic, konkrétně světla, tedy fotonů. Co je to vlastně polarizace? K čemu slouží? Nejjednoduššeji si ji lze představit prostřednictvím obrázku. Mějme nějaký zdroj nepolarizovaného světla — např. žárovku, LED[5]Nikdy prosím nepište LED diodu, to je jazykově špatně., něco takového.
 Z tohoto zdroje se šíří nepolarizované světlo, tzn. že nemá žádnou “polaritu”. Tím je myšleno, že jeho vlny jdou “ve všech směrech” současně. Neplést s nehomogenním světelným zdrojem, což je zdroj, který vysílá světlo “na všech frekvencích”. Světelný zdroj tedy může být polarizovaný homogenní, nepolarizovaný homogenní, polarizovaný nehomogenní a nepolarizovaný nehomogenní.
Z tohoto zdroje se šíří nepolarizované světlo, tzn. že nemá žádnou “polaritu”. Tím je myšleno, že jeho vlny jdou “ve všech směrech” současně. Neplést s nehomogenním světelným zdrojem, což je zdroj, který vysílá světlo “na všech frekvencích”. Světelný zdroj tedy může být polarizovaný homogenní, nepolarizovaný homogenní, polarizovaný nehomogenní a nepolarizovaný nehomogenní.
Abychom takové světlo “zpolarizovali”, potřebujeme nějaký polarizátor, případně polarizační filtr. Polarizační filtr je zařízení, které propustí světlo pouze které má nějakou konkrétní polarizaci. Pro zjednodušení si nyní určeme tři základní směry:
- doprava a doleva se budeme pohybovat po ose \(x\). Světlo polarizovaní po ose \(x\) bude světlo s horizontální polarizací
- nahoru a dolů se budeme pohybovat po ose \(y\). Světlo takto polarizované bude mít vertikální polarizaci.
- dopředu a dozadu se nacházíme na ose \(z\). Světlo takto polarizované bude mít taktéž horizontální polarizaci.
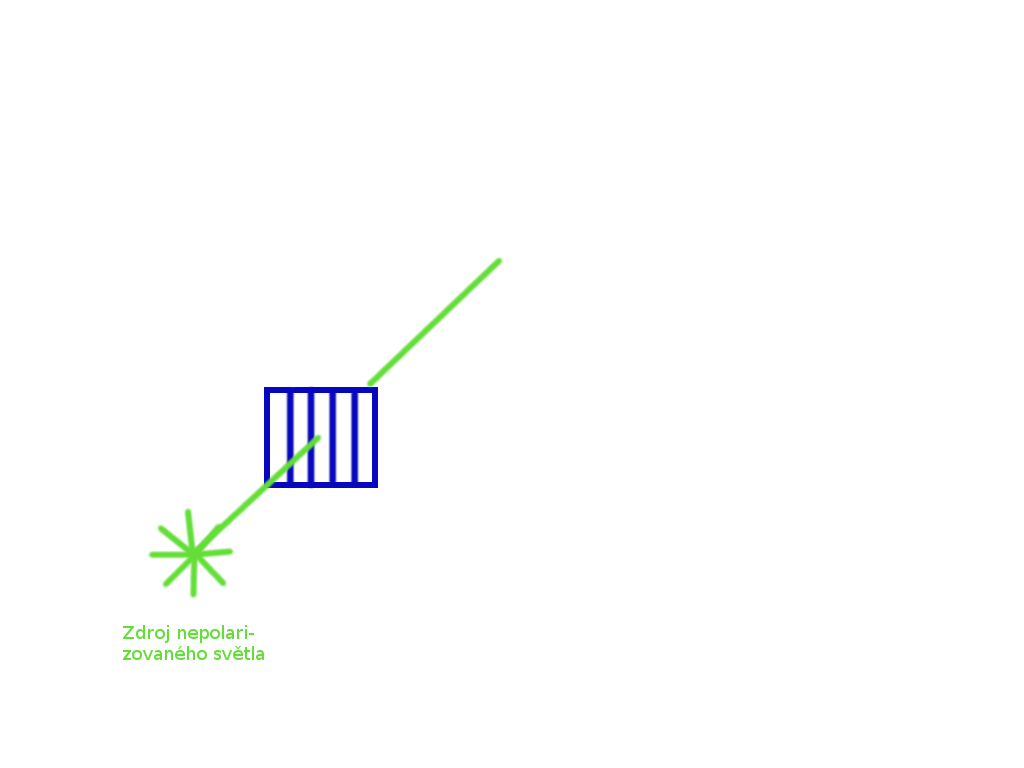
Pro zjednodušení však nejdříve budeme uvažovat pouze dva směry, tedy doprava/doleva a nahoru/dolů. Přidejme proto do našeho situačního plánku takový polarizační filtr a pošleme skrz něho paprsek světla:
Tento paprsek bude mít po průchodu takovým polarizátorem vertikální polarizaci, tedy bude mít polarizaci po ose \(y\). Pokud bychom nyní zkoušeli, co se s takovým paprskem dále stane, zařadíme-li do něho další polarizátor, zjistíme, že zařadíme-li další vertikální \(y\) polarizátor, světlo neztratí nic ze své intenzity[6]samozřejmě v ideálních podmínkách s ideálními filtry atd. a bude mít intenzitu 100 % intenzity před druhým filtrem:
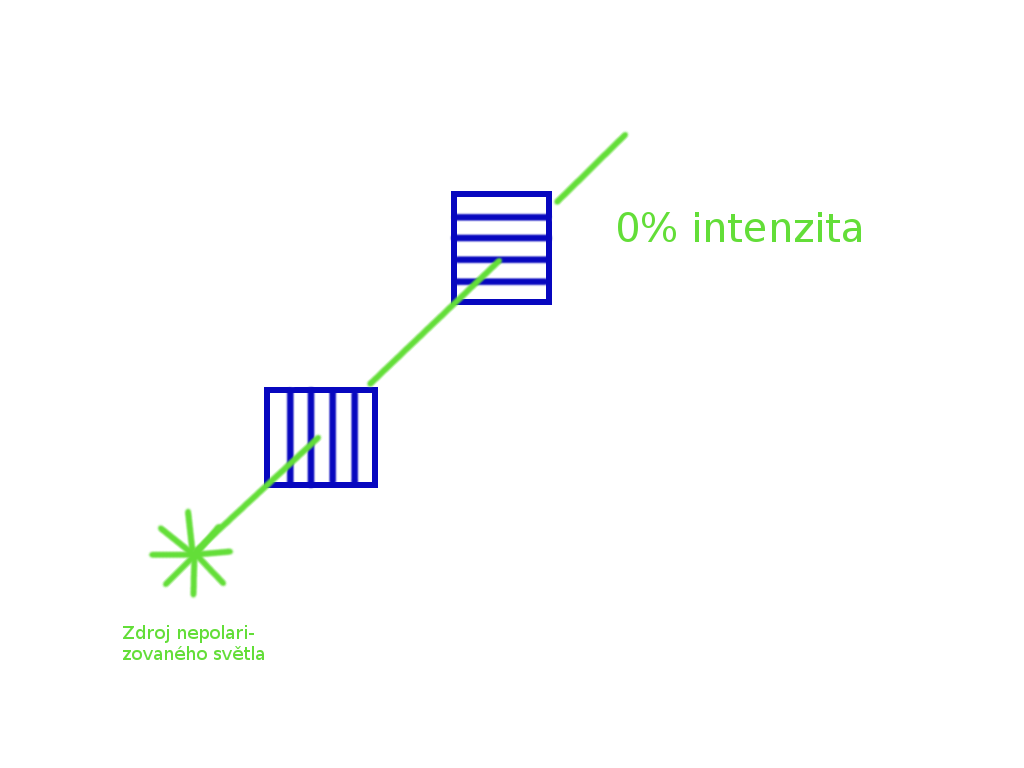
Naopak pokud druhý filtr otočíme o 90 °, bude výstupem 0% intenzita — všechno světlo se během sekundární polarizace ztratí:
Pokud budeme s druhým filtrem různě otáčet, dostane se nám různé vělkých intenzit na výstupu takové kaskády; tyto intenzity budou dokonce záviset přímo na rozdílu úhlu těchto filtrů, konrétně faktorem \(\cos^2(\alpha)\). Nicméně zde končí běžný “makroskopický” svět našich dobře nám známých představ.
Když si totiž uvědomíme, že intenzita světla odpovídá \(I = \mathrm{k}E^2\), potom by mohlo vypadat, že s klesající intenzitou bude klesat i energie záření — a tím podle známého \(E=hf\) by měla klesat i frekvence záření. Nicméně to se neděje. A již za okamžik si vysvětlíme proč — jedná se totiž o kvantové jevy, které jsou pro člověka, který je zvyklý na běžné makroskopické jevy, poměrně nepřirozené.
Je nutné nad světlem (byť polarizovaným) uvažovat jako nad proudem částic. Druhý polarizátor nedělá nic jiného, než že propustí ty fotony, které splňují podmínky propuštění a “zamítne” fotony, které nesplňují takové podmínky. Avšak ty fotony, které propustí, těm energii nemění. Nenastává tedy změna energie fotonu, pouze množství fotonů, které se propustí. A to je dost zásadní rozdíl.
Pojďme se nyní podívat, jak funguje světlo jako proud částic. Využijme k tomu výše uvedených dvou polarizačních filtrů. Již jsme si představili bra a ket vektory, nyní je můžeme využít prakticky. Trošku “ze vzduchu” nyní vypustím jeden důležitý vztah — který shodou okolností krásně popisuje kvantové jevy:
$$H|a\rangle=\lambda|a\rangle$$
Rovnice[7]Někdo v tom zajisté uvidí emotikonu vyjadřující předek autobusu 🙂 vyjadřuje, jakým způsobem se chovají částice v mikrosvětě. Zkusme nyní pomocí této rovnice vyjádřiv výše uvedené situace s dvěma polarizačními filtry. Ze začátku budu házet trochu “náhodné” hodnoty do matic, prosím zatím mi důvěřujte, postupně se dostanu i k jejich vyjádření, nyní však chci, abychom se podívali prakticky na využití rovnice.
Co jednotlivé komponenty rovnice znamenají? Nyní jen stručně:
- \(\langle{}H|\) vyjadřuje matici[8]o které se časem dozvíme, že je Hermitovská, která vyjadřuje nějaké “hodnoty v experimentu”.
- \(|a\rangle\) je tzv. vlastní vektor, který určuje stav systému.
- \(\lambda\) je tv. vlastní číslo, které určuje výstup z experimentu.
- \(|a\rangle\) je opět ten stejný vlastní vektor, jako o několik bodů výše. Všimněme si, že tento vektor je opravdu stejný jako na začátku reakce.
Pokud budeme tedy uvažovat vertikálně polarizované světlo (či proud částic obecně) a přiřadíme následující vektory:
- horizontální polarizace: \(|x\rangle= \begin{pmatrix}1\\0\end{pmatrix}\)
- vertikální polarizace: \(|y\rangle= \begin{pmatrix}0\\1\end{pmatrix}\)
Můžeme se ptát následujícím bra-ketovým zápisem:
$$\langle{}x|y\rangle$$
Tedy slovy: Jaká je pravděpodobnostní amplituda, že připravíme-li částici, která bude mít \(y\) polarizaci, projde taková částice filtrem s \(x\) polarizací? Samozřejmě se můžeme ptát pak i obecně na libovolný úhel, ale o tom až později.
Proč však pouze “pravděpodobností amplituda”? Protože abychom získali pravděpodobnost, musíme použít:
$$\langle{}x|y\rangle\langle{}y|x\rangle$$
Nicméně jak jsme ukázali výše, toto se dá zapsat i jako:
$$\langle{}x|y\rangle\langle{}x|y\rangle^*$$
Využijeme tedy komplexně sdružených čísel. Budeme-li však uvažovat pouze reálná čísla, kde je imaginární složka nulová, můžeme pak s klidným svědomím psát, že pravděpodobnost takového jevu je:
$$\langle{}x|y\rangle^2$$
Zpět k praktickému příkladu — jaká je tedy pravděpodobnost, že horizontálně polarizovaná částice projde filtrem s vertikální polarizací?
$$ \langle{}x|y\rangle^2 = \begin{pmatrix}1 & 0\end{pmatrix}^* \begin{pmatrix}0\\1\end{pmatrix} = 0$$
Výpočet tedy odpovídá realitě, protože pro kolmé roviny polarizace částice a polarizačního filtru, je pravděpodobnost opravdu nulová.
Stejně tak zjistíme, že pro stejnou polarizaci částice i směr filtru dostaneme:
$$ \langle{}x|y\rangle^2 = \begin{pmatrix}1 & 0\end{pmatrix}^* \begin{pmatrix}1\\0\end{pmatrix} = 1$$
Čili opět odpovídající stav realitě — v takovém případě máme 100% pravděpodobnost, že taková částice projde.
Vraťme se nyní k našemu (starému známému) \(H|a\rangle=\lambda|a\rangle\).
Nyní opět “vystřelím” do vzduchu a napíšu, jak takové \(H\) vypadá, vysvětlení však přijde později (odvození). Myslím si, že pro pochopení toho, jak to odvodit, je dobré nejdříve vědět, jak tato “věc” funguje. Potom už je odvození otázka chvilky 🙂
Řekněme, že tato Hermitovská matice má tvar \(\begin{pmatrix}1&0\\0&-1\end{pmatrix}\).
Potom, co uděláme \(H|x\rangle=\lambda|x\rangle\) zjistíme, že:
$$\begin{pmatrix}1 & 0\\0 & -1\end{pmatrix}\begin{pmatrix}1\\0\end{pmatrix}$$
můžeme vyřešit jako:
$$\begin{pmatrix}1 & 0\\0 & -1\end{pmatrix}\begin{pmatrix}1\\0\end{pmatrix}=\begin{pmatrix}1\cdot1 + 0\cdot 0 \\ 0 \cdot 1 – 1 \cdot 0\end{pmatrix} = \begin{pmatrix}1 \\ 0\end{pmatrix}$$
Podíváme-li se na výše uvedenou formuli:
$$\color{blue}H|\color{red}a\rangle=\color{pink}\lambda|\color{red}a\rangle$$
a zapíšeme-li maticově tedy jako:
$$\color{blue}{\begin{pmatrix}1 & 0\\0 & -1\end{pmatrix}}\color{red}{\begin{pmatrix}1\\0\end{pmatrix}}=\color{red}{\begin{pmatrix}1 \\ 0\end{pmatrix}}$$
a tedy pouze doplníme \(\color{pink}\lambda\) a získáme:
$$\color{blue}{\begin{pmatrix}1 & 0\\0 & -1\end{pmatrix}}\color{red}{\begin{pmatrix}1\\0\end{pmatrix}}=\color{pink}\lambda\color{red}{\begin{pmatrix}1 \\ 0\end{pmatrix}}$$
Vidíme, že \(\lambda=1\). Nyní se zkusme podívat, co se stane, pokud použijeme ket \(|y\rangle\):
$$\color{blue}{\begin{pmatrix}1 & 0\\0 & -1\end{pmatrix}}\color{red}{\begin{pmatrix}0\\1\end{pmatrix}}=\color{pink}\lambda\color{red}{\begin{pmatrix}0 \\ 1\end{pmatrix}}$$
Spočítáme-li součin hermitovské matice a ketu na levé straně rovnice, dostaneme:
$$\begin{pmatrix}1 & 0\\0 & -1\end{pmatrix}\begin{pmatrix}0\\1\end{pmatrix}=\begin{pmatrix}1\cdot0 + 0\cdot 1 \\ 0 \cdot 0 – 1 \cdot 1\end{pmatrix} = \begin{pmatrix}0 \\ -1\end{pmatrix}$$
Abychom tedy dostali stejný vlasní vektor vpravo i vlevo, vlastní číslo \(\lambda\) musí být \(\color{pink}{\lambda=-1}\) a tedy:
$$\color{blue}{\begin{pmatrix}1 & 0\\0 & -1\end{pmatrix}}\color{red}{\begin{pmatrix}0\\1\end{pmatrix}}=\color{pink}{-1}\color{red}{\begin{pmatrix}0 \\ 1\end{pmatrix}}$$
Co nám tedy hodnota \(\lambda\) říká? Prakticky si ji můžeme představit jako “krabičku”[9]Prostě blackbox 🙂 , která nám nějakým indikátorem (třeba LED) říká, jestli to, co nastavujeme (stav systému, tedy ket) je v experimentu (zde bra) potvrzeno (\(\lambda\)) či nikoliv.
Polarizace s obecným úhlem
Zkusme se nyní podívat na situaci, kdy máme nějakým směrem (ať už horizontálně či vertikálně) polarizovaný paprdek svěla a proženeme ho polarizátorem, který je natočený nějakým obecným úhlem \(\phi\).
Začněme nejdříve trošku “méně obecnou” variantou, vlastně docela dost konkrétní — nastavme polarizační filtr pod úhlem 45 °. Jenže — vyvstává problém, jak vektorově reprezentovat možnost natočení pod tímto úhlem. Nabízí se (ne až tak špatné) řešení, které má však své drobné úskalí, jež ale velmi záhy překonáme a vyřešíme.
Představme si tedy nyní situaci, kdy máme vertikálně polarizovaný paprsek světla a postavíme před něho polarizátor v úhlu 45 ° “doprava” — tedy jako lomítko “/” 🙂 Jakým způsobem tedy reprezentovat toto “lomítko?” Dalo by se říci (přiblížit se cíli), že pokud je polarizátor pod takovýmto úhlem, je nastaven vlastně “někde akorát mezi” — tedy ani ne moc horizontálně, ale ani ne moc vertikálně.
Mohli bychom tedy zkusit vyslovit hypotézu, že výsledná polarizace bude něco jako součet horizontálního a vertikálního polarizátoru — tedy něco jako \(|x\rangle + |y\rangle\). To je poměrně dobrá myšlenka, ale přivádí nám některá úskalí, která si nyní ukážeme.
Víme, že vlastní vektory jsou vektory[10]Už jen proto, že se tak jmenují, ale hlavně se tak i chovají 🙂 , takže s nimi můžeme dělat i běžné vektorové operace, jako třeba součet:
$$\color{blue}{|x\rangle} + \color{violet}{|y\rangle} =
\color{blue}{\begin{pmatrix} 1 \\ 0 \end{pmatrix}}+\color{violet}{\begin{pmatrix} 0 \\ 1\end{pmatrix}}
=\begin{pmatrix} 1 \\ 1 \end{pmatrix}$$
Nyní však experiment — pokud vezmeme světlo polarizované pod úhlem 45 ° a proženeme ho filrem pod stejným úhlem, musí nám vyjít, že máme opět 100 % světla, která jsme tam vpustili, i na druhé straně, tedy označíme-li takový polarizační filtr jako \(|/\rangle\) a zdroj světla jako \(\langle/|\), dostaneme:
$$\left(|\langle{}/|/\rangle{}|\right)^2=\left(\begin{pmatrix}1 & 1\end{pmatrix}\begin{pmatrix} 1 \\ 1 \end{pmatrix}\right)^2 = 2^2 = 4$$
Čili, jak vidíme, vyjde nám 400% pravděpodobnost, že foton projde. To je sice dost působivé, nicméně potřebovali bychom (tak nějak logicky) dostat, že nám prostě vyjde 100 %. A toho docílíme metodou normalizace.
Nejjednoduššeji bychom řekli, že chceme ze čtyřky udělat jedničku, takže prostě podělíme čtyřmi a máme jedničku — ve své podstatě vlastně ano, ale pokud bychom si chvilku s vektry hráli a zjišťovali, čím vstup podělit, aby na výstupu bylo 4krát menší číslo, přišli bychom na vztah:
$$\frac{|x\rangle + |y\rangle}{\sqrt{2}}$$
Zkusme nyní ověřit:
$$\begin{pmatrix}\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\end{pmatrix}\begin{pmatrix}\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{pmatrix}=\frac{1}{\sqrt{2}}\cdot\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}\cdot\frac{1}{\sqrt{2}} = \frac{1}{2} + \frac{1}{2} = 1$$
Skvělé! Takže máme předpis, který pro takovou polarizaci můžeme použít. Zcela intuitivně též odhadneme, jak bude vypadat vzorec pro polarizační filtr o 45 ° na druhou stranu, tedy jako lomítko “\” — vertikální složka (tedy \(|x\rangle\)) zůstane stejná, horizontální složka bude opačná (tedy \(-|y\rangle\)):
$$\frac{|x\rangle – |y\rangle}{\sqrt{2}}=\begin{pmatrix}\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}}\end{pmatrix}$$
Nyní tedy zkusme, jak by dopadlo, pokud bychom vzali polarizované světlo ve směru “opačného lomítka \” a pustili ho přes filtr “běžného lomítka /?” Víme, že výsledek musí být nulový, ověřme proto funkci:
$$
|\left\langle\color{red}/|\color{violet}\setminus\right\rangle|^2=
\left(
\color{red}{\begin{pmatrix}\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\end{pmatrix}}
\color{violet}{\begin{pmatrix}\frac{1}{\sqrt{2}}\\-\frac{1}{\sqrt{2}}\end{pmatrix}}
\right)^2=
\left(
\color{red}{\frac{1}{\sqrt{2}}}\cdot\color{violet}{\frac{1}{\sqrt{2}}}-
\color{red}{\frac{1}{\sqrt{2}}}\cdot\color{violet}{\frac{1}{\sqrt{2}}}
\right)^2=0
$$
Nyní, když víme, že naše vektory pro zápis polarizačního filtru jsou funkční, můžeme opět stejně, jako jsme měli výše, provést pokus s Hermitovskou maticí[11]tentokrát trochu jinou, později se opravdu dostanu k odvození toho, proč zrovna takovou 🙂 :
$$
H|/\rangle=\lambda|/\rangle
\\
\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}
\cdot
\begin{pmatrix}
\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}
\end{pmatrix}
=
\begin{pmatrix}
\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}
\end{pmatrix}
=
\lambda\cdot
\begin{pmatrix}
\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}
\end{pmatrix}
$$
Vidíme tedy, že vlastní vektory se opět rovnají, a tedy \(\lambda=1\) taktéž.
Krátké shrnutí
Shrňme si nyní v krátkosti, jak vypadají jednotlivé vektory pro různé úhly polarizace:
- Vertikální polarizace, tedy “|” : \(0|x\rangle+1|y\rangle=\begin{pmatrix}0 \\ 1\end{pmatrix}\)
- Horizontální polarizace, tedy “–” : \(1|x\rangle+0|y\rangle=\begin{pmatrix}1 \\ 0\end{pmatrix}\)
- Šikmá polarizace “/” : \(\frac{1}{\sqrt{2}}|x\rangle+\frac{1}{\sqrt{2}}|y\rangle=\begin{pmatrix}\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{pmatrix} \)
- Šikmá polarizace “\” : \(\frac{1}{\sqrt{2}}|x\rangle-\frac{1}{\sqrt{2}}|y\rangle=\begin{pmatrix}\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}}\end{pmatrix} \)[12]Ve své podstatě je téměř jedno, jestli dáte do záporu \(x\) nebo \(y\), protože výsledek bude prakticky stejný — stejně jako je jedno, jestli uděláte při např. vertikální polarizaci opačně \(y\), pro světlo je to jedno 🙂
Možná už je trošku z tohoto shrnutí vidět, co vlastně reprezentují jednotlivá čísla zapsaná v těchto takto zapsaných vlastních vektorech. Jedná se (opět, narazili jsme na to ze začátku textu) o pravděpodobnostní amplitudu, což je neměřitelná veličina, která právě v kvantovém světě popisuje krásně tyto jevy. Pokud umocníme absolutní hodnotu této veličiny na druhou, dostaneme pravděpodobnost, jakou projde částice filtrem právě s takovou pravděpodobnostní amplitudou.
Jak je to tedy s obecným vztahem pro obecný úhel?
Podívejme se nyní na to, jak bychom obecně vyjádřili vlastní vektor pro obecný úhel. Podíváme-li se na běžný graf, kde jsem zakreslil nějaký obecný jednotkový vektor pod úhlem \(\phi\)…
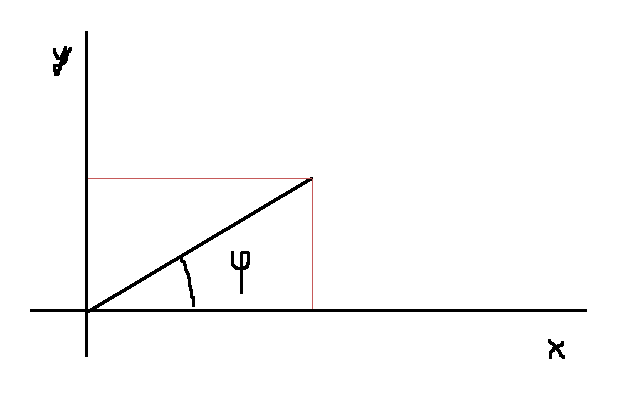
Dá nám smysl, že tento jednotkový vektor vytkne na ose \(x\) právě \(\cos{\phi}\) a na ose \(y\) právě \(\sin{\phi}\) jednotek těchto os. Zkusme tedy předpokládat, že bychom mohli tvrdit následující (což vypadá poměrně logicky):
$$
|\phi\rangle=
\begin{pmatrix}
\cos{\phi}\\\sin{\phi}
\end{pmatrix}
=
\cos{\phi}|x\rangle + \sin{\phi}|y\rangle
$$
Stejně jako u všech vektorů, pokud chceme vytvořit kolmý vektor (v tomto případě dokonce ortogonální, tedy takový, který má přesně opačné vlastnosti jako první vektor[13]Či lidově — vše, co je tuto, přesně není tamto 😀 ), uděláme “trik” s prohozením a otočením, tedy obecně vektor \(\begin{pmatrix}x \\ y\end{pmatrix}\) převedeme na \(\begin{pmatrix}y \\ -x\end{pmatrix}\). Nazvěme si tedy náš první vektor kupříkladu \(\phi_{\alpha}\) a náš druhý \(\phi_{\beta}\):
$$
\phi_{\alpha}=
\begin{pmatrix}
\cos{\phi}\\\sin{\phi}
\end{pmatrix}
$$
$$
\phi_{\beta}=
\begin{pmatrix}
\sin{\phi}\\-\cos{\phi}
\end{pmatrix}
$$
Ověřme nyní hypotézu o průchodu dvěma polarizátory (případně hypotézu o průchodu polarizovaných fotonů kolmo orientovaným polarizátorem):
$$
\left\langle \phi_{\alpha}|\phi_{\beta}\right\rangle=
\begin{pmatrix}
\cos{\phi} & \sin{\phi}
\end{pmatrix}
\begin{pmatrix}
\sin{\phi} \\ -\cos{\phi}
\end{pmatrix}
=
\cos{\phi}\sin{\phi}-\sin{\phi}\cos{\phi}
=
0
$$
Tedy potvrzeno 🙂 Zkusme pro jistotu ještě dvě stejnosměrné polarizace:
$$
\left\langle \phi_{\alpha}|\phi_{\alpha}\right\rangle=
\begin{pmatrix}
\cos{\phi} & \sin{\phi}
\end{pmatrix}
\begin{pmatrix}
\cos{\phi} \\ \sin{\phi}
\end{pmatrix}
=
\cos{\phi}\cos{\phi}+\sin{\phi}\sin{\phi}
=
\cos^2{\phi}+\sin^2{\phi}
=
1
$$
Nyní se podívejme, jaká pravděpodobnost průchodu částice bude, pokud připravíme částici s obecnou polarizací pod úhlem \(\phi\) a polarizační filtr nastavíme horizontálně:
$$
\left(
|
\left\langle x | \phi \right\rangle
|
\right)^2
=
\left(
\begin{pmatrix}
1 & 0
\end{pmatrix}
\begin{pmatrix}
\cos{\phi} \\ \sin{\phi}
\end{pmatrix}
\right)^2
=
\left(
1\cdot\cos{\phi} + 0\cdot\sin{\phi}
\right)^2
=
\cos^2{\phi}
$$
No, tak výborně 🙂 Stejným způsobem bychom mohli spočítat pravděpodobnost průchodu, pokud není polarizační filtr nastaven horizontálně, ale vertikálně, vyjde to prostě stejně. Nyní tedy nezbývá než udělat naprosto obecný případ.
Mějme tedy zdroj nějakého světla, který proženeme dvěma polarizačními filtry, každý nastaven pod určitým obecným úhlem, první např. pod úhlem \(\phi_\alpha \) a druhý pod úhlem \(\phi_\beta\). Podrobme naše výpočty tomuto testu. Nejprve tedy připravíme světelný paprsek filtrem \(\phi_\alpha\), poté pokračujeme dále k filtru \(\phi_\beta\):
$$
\left|
\left\langle\beta|\alpha\right\rangle
\right|^2
=
\left(
\begin{pmatrix}
\cos\beta & \sin\beta
\end{pmatrix}
\begin{pmatrix}
\cos\alpha \\ \sin\alpha
\end{pmatrix}
\right)^2
=
\left(
\cos\beta\cos\alpha + \sin\beta\sin\alpha
\right)^2
=
\cos(\alpha-\beta)^2
$$
Možná se budete divit, jak jsem se dostal k poslednímu kroku — je to nějaký vzoreček, stejně jako \(\cos^x+\sin^2x=1\), platí i tento vzoreček 🙂 Dále — proč tam není rozdíl úhlů třeba opačný — opět, je to jedno, protože platí \(\cos{x}=\cos{-x}\).
Tím jsme si tedy potvrdili funkci těchto “stavebních bloků”. Vraťme se nyní na chvilku k původnímu vzorci:
$$ H|a\rangle=\lambda|a\rangle$$
A právě k Hermitovské matici \(\hat{H}\). Výše jsme si ukázali nějaké příklady na tuto matici, nicméně zkusme ji nyní trošku zobecnit. Nejprve napíšu, jak “to s ní vypadá” a poté rozebereme, co se s takovou maticí dá dále dělat 🙂
$$
\hat{H}=
\begin{pmatrix}
\cos2\phi & \sin2\phi \\
\sin2\phi & -\cos2\phi
\end{pmatrix}
$$
Existují dva “vzorečky”, které zde využijeme:
$$\cos2\phi=\cos^2\phi-\sin^2\phi$$
$$\sin2\phi=2\sin\phi\cos\phi$$
Těch zde využijeme a přepíšeme do matice. Pro zjednodušení teď vynechám neustálé psaní \(\phi\) a \(2\phi\):
$$
\hat{H}=
\begin{pmatrix}
\cos2\phi & \sin2\phi \\
\sin2\phi & -\cos2\phi
\end{pmatrix}
=
\begin{pmatrix}
\cos^2-\sin^2 & 2\cos\sin \\
2\cos\sin & \sin^2 – \cos^2
\end{pmatrix}
$$
Použijeme-li tedy předpisu \(\hat{H}|\phi\rangle=\lambda|\phi\rangle\) a použijeme-li v něm nám již známé prvky, dostaneme:
$$
\hat{H}|\phi\rangle=\lambda|\phi\rangle
\\
\begin{pmatrix}
\cos^2-\sin^2 & 2\cos\sin \\
2\cos\sin & \sin^2 – \cos^2
\end{pmatrix}
\begin{pmatrix}
\cos \\ \sin
\end{pmatrix}
=
\lambda
\begin{pmatrix}
\cos \\ \sin
\end{pmatrix}
$$
Mělo by tedy platit, že produkt na levé straně bude stejný jako vektor na pravé straně. Udělejme tedy několik základních algebraických úprav:
$$
\begin{pmatrix}
\cos^2-\sin^2 & 2\sin\cos \\
2\sin\cos & \sin^2-\cos^2
\end{pmatrix}
\begin{pmatrix}
\cos \\ \sin
\end{pmatrix}
=
\begin{pmatrix}
\cos^3-\sin^2\cos+2\sin^2cos \\
2\cos^2\sin + \sin^3 – \cos^2\sin
\end{pmatrix}
= \\ =
\begin{pmatrix}
\cos^3+\sin^2\cos \\
\cos^2\sin + \sin^3
\end{pmatrix}
=
\begin{pmatrix}
\cos\left(\cos^2+\sin^2\right) \\
\sin\left(\cos^2+\sin^2\right)
\end{pmatrix}
=
\begin{pmatrix}
\cos \\
\sin
\end{pmatrix}
$$
Vidíme tedy, že produkt na levé straně je opravdu stejný, jako vektor na straně pravé, vlastní číslo je tedy \(\lambda=1\) 🙂 Stejně tak to bude fungovat i pokud použijeme vektoru ortogonálního, tedy \(\begin{pmatrix}-\sin \\ \cos\end{pmatrix}\), jen samozřejmě vyjde \(\lambda=-1\) dle očekávání — kolmý filtr na rovinu polarizace nepropustí nic.
Další pokračování článku
V dalším pokračování článku, která vydám v nedaleké budoucnosti, se budeme věnovat zvláštnímu typu polarizace, tedy kruhové polarizaci, potom spinu částice a dalším zajímavostem, tak se těšte 🙂
Poznámky pod čarou
| ⇧1 | Protože pokud chceme pochopit spin, musíme pochopit i ten zbytek. |
|---|---|
| ⇧2 | či Diracovou, ale to se mi dost příčí |
| ⇧3 | Pro potřeby tohoto článku budu označovat takto, nicméně skalární součin normálně funguje bez komplexně sdružených čísel, takže toto ve své podstatě není “až tak” běžný skalární součin. Správně bych měl třeba nazývat konjugovaný sk. součin, ale jsem moc líný to psát takto dlouhé — proto odteď budu psát pouze “skalární součin”. Děkuji za pochopení. |
| ⇧4 | Pro další informace doporučuji bezvadný zdroj všech možných matematických informací — web MatFyzu :-): http://wiki.matfyz.cz/index.php?title=16._Formalizmus_kvantov%C3%A9_teorie |
| ⇧5 | Nikdy prosím nepište LED diodu, to je jazykově špatně. |
| ⇧6 | samozřejmě v ideálních podmínkách s ideálními filtry atd. |
| ⇧7 | Někdo v tom zajisté uvidí emotikonu vyjadřující předek autobusu 🙂 |
| ⇧8 | o které se časem dozvíme, že je Hermitovská |
| ⇧9 | Prostě blackbox 🙂 |
| ⇧10 | Už jen proto, že se tak jmenují, ale hlavně se tak i chovají 🙂 |
| ⇧11 | tentokrát trochu jinou, později se opravdu dostanu k odvození toho, proč zrovna takovou 🙂 |
| ⇧12 | Ve své podstatě je téměř jedno, jestli dáte do záporu \(x\) nebo \(y\), protože výsledek bude prakticky stejný — stejně jako je jedno, jestli uděláte při např. vertikální polarizaci opačně \(y\), pro světlo je to jedno 🙂 |
| ⇧13 | Či lidově — vše, co je tuto, přesně není tamto 😀 |

1 komentář u „Polarizace a spin částice (1. část)“
Komentáře nejsou povoleny.