Na základě diskuse na Facebooku, kde se kamarád pokoušel pochopit z mých krátkých příspěvků, jak souvisí výkon a kroutivý moment, jsem se raději rozhodl sepsat myšlenky do plnohodnotného (byť krátkého) článku. Zcela věřím, že totiž tento kamarád nebude jediný, kdo má v uvedených pojmech jakousi “mlhu” a potřeboval by je osvětlit.

Výkon, kroutivý moment a jejich význam

Všechny motory máme na světě proto, aby konaly nějakou práci. Práce, uváděná v Joulech, je veličina, která nám popisuje doslova “kolik je toho třeba udělat”. Kupříkladu pokud budeme táhnout 500kilový klavír do 4. patra, tedy zhruba do 20 metrů výšky, budeme potřebovat přibližně (zaokrouhlujme prosím) práci:

$$W=F s = m g s = 500 \cdot 10 \cdot 20 = 100\ \mathrm{kJ}$$

(ke stejnému výsledku bychom došli, kdybychom počítali přes potenciální energii, kde \(W = mgh\), což je vlastně totéž v našem případě 😉 )

Abychom tedy dostali takový klavír do takového 4. patra, potřebujeme někde sehnat práci \(100\ \mathrm{kJ}\). Buď ji vyvineme ručně, kladkami či použijeme nějaký motor. Jenže samozřejmě intuitivně, pokud budeme mít motor, který bude mít “větší páru”, vytáhne nám tam klavír mnohem rychleji než nějaký slaboučký motůrek. Množství toho, jakou “to má páru” se tedy říká výkon a jedná se velmi jednoduše po schopnost provést nějakou práci za průměrný čas. Pokud bychom tedy chtěli náš klavír vytáhnout za 10 vteřin, budeme potřebovat výkon:

$$ P = \frac{W}{t} = \frac{m g s}{t} = \frac{500 \cdot 10 \cdot 20}{10} = 10\ \mathrm{kW}$$

Budeme tedy potřebova motor s výkonem alespoň \(10\ \mathrm{kW}\). Samozřejmě nebudeme uvažovat, že motory nemají 100% účinnost a tak podobně, spíše jde o princip jako takový.

Nicméně — je vám asi jasné, že úplně “nefunguje” jednoduchá zkratka, že pokud vezmu třeba motorek z ostřikovačů a budu s ním zvedat takový klavír, bude mi to trvat třeba 2 hodiny a zvednu ho.  Samozřejmě by to mohlo fungovat, ale je potřeba, aby — byť pomalý — motor uměl vykonávat nějakou sílu, která by byla větší, než síla působící gravitací (tedy aby klavír neklesal, ale stoupal).

Musí být tedy schopen vyvinout určitý moment, kterým by na dané těleso působil (byť pomalu). Jedná se o točivý stroj (motor se otáčí a dělá pořád dokola to samé — zabírá), veličina, která nám popisuje toto silové působení se nazývá kroutivý moment.

Pokud definujeme dráhu, kterou musí obvod točivého stroje (jeho aktivní části) vykonat, aby udělal jednu otáčku, je to klasický obvod:

$$o=\frac{2\pi o}{60}$$

Šedesáti dělíme proto, že otáčky se uvádí v “rpm”, tedy “otáčkách za minutu”. Pokud máte otáčky v otáčkách za sekundu, poté samozřejmě nedělíte 🙂 Práce, jak víme, je silové působení po nějaké dráze, tedy:

$$ W = F s$$

No a pokud víme, že dráha je rovna obvodu:

$$ W = F s = F \frac{2 \pi r}{60}$$

Což je náš vztah pro výkon. Můžeme udělat zkratku, že:

$$M = F r$$

A tedy

$$ W = \frac{2 \pi M o}{60}$$

Daný výkon motoru tedy přímo souvisí s kroutivým momentem, kterým motor na danou “překážku” působí.

Praktické otázky

Vidíme, že výkon motoru je přímo závislý na otáčkách motoru. Zkusme si proto zaexperimentovat s různými průběhy kroutivého momentu a výkonu.

Příklad 1) Plochý “kroutivý moment”:

Průběh kroutivého momentu tedy bude vypadat např. takto:

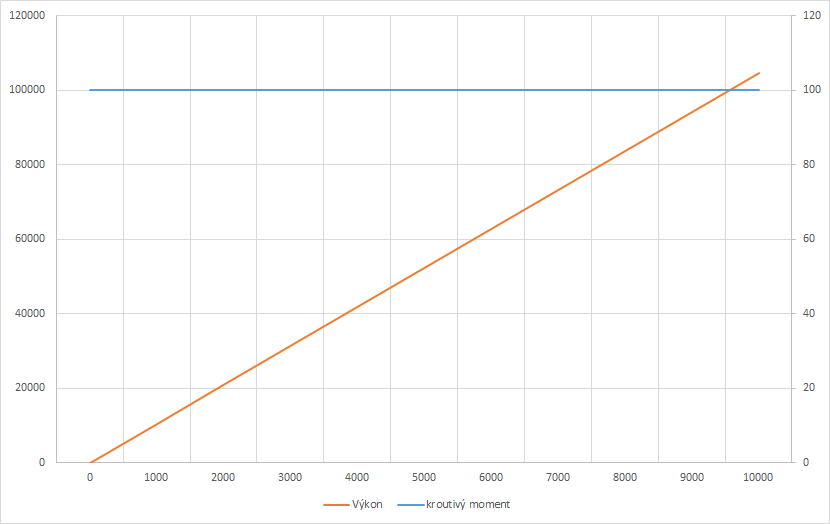
Vidíme, že motor, který by měl takto rovný průběh, by dosahoval největších výkonů při nejvyšších otáčkách, přičemž by měl stále konstantní kroutivý moment, v našem případě \(100\ \mathrm{Nm}\). Osa výkonu je ve Wattech, tedy vidíme, že kolem 10 000 otáček by měl motor výkon přes 100 kW, což odpovídá zhruba 135 koňským silám.

Žádný motor však nemá takto krásný průběh krouťáku, možná tak v Tesle se přibližují, ale jinak se jedná většinou o nějakou křivku. V technických specifikacích motoru většinou najdete, že máte “maximální krouťák” třeba 110 Nm při 4500 otáčkách. To znamená, že všude jinde je to “méně”. Zkusme si tuto situaci opět načrtnout grafem:

Příklad 2) Motor s reálným krouťákem

 

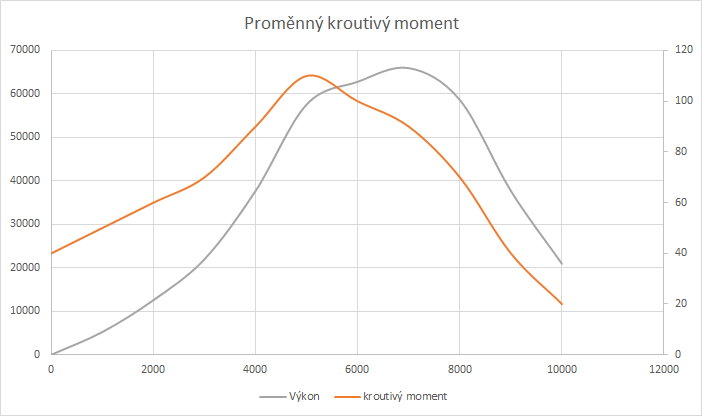
Zde vidíme zajímavý jev — zatímco kroutivý moment má svůj vrchol zhruba v oněch 5000 otáčkách, výkon má svůj vrchol skoro až v 7000. Tyto charakteristiky jsou právě velmi důležité — čím máte vyšší krouťák ve vyšších otáčkách, tím máte i větší výkon.

Doufám, že je to vše jasné, případně se ozvěte do komentů 😉 A budu rád za sdílení! 😉