Příklad s goniometrickými funkcemi pro Jarmilu 🙂 Anebo jak dostat ze \(\sin 2x = -\frac{\sqrt{3}}{2}\) ono \(x\)? 🙂

Co nám tuto zadání vlastně říká? K řešení máme už veškeré podklady; víme, jak vypadá graf funkce \(\sin x\), jak však vypadá graf funkce \(\sin 2x\)?

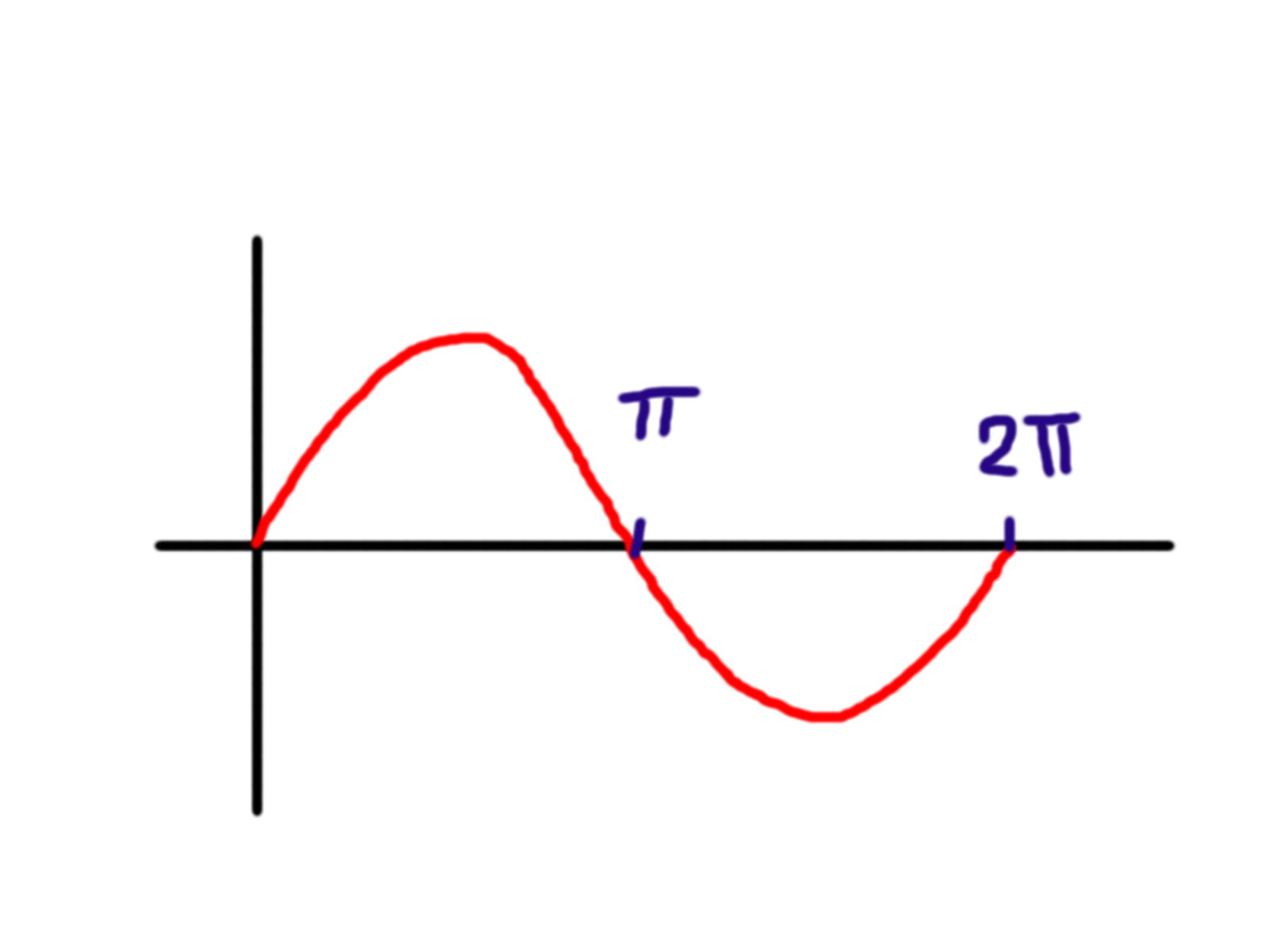
Výchozí funkce \(y(x)=\sin x\) tedy vypadá takto:

Funkce \(y(x) = \sin 2x\) vypadá úplně stejně, akorát má dvakrát větší frekvenci, což znamená totéž, jako když řeknu, že má dvakrát menší periodu. Křivka tak necestuje od \(0\) do \(2\pi\), ale jen do \(\pi\).

Vypadá to tedy nějak následovně:

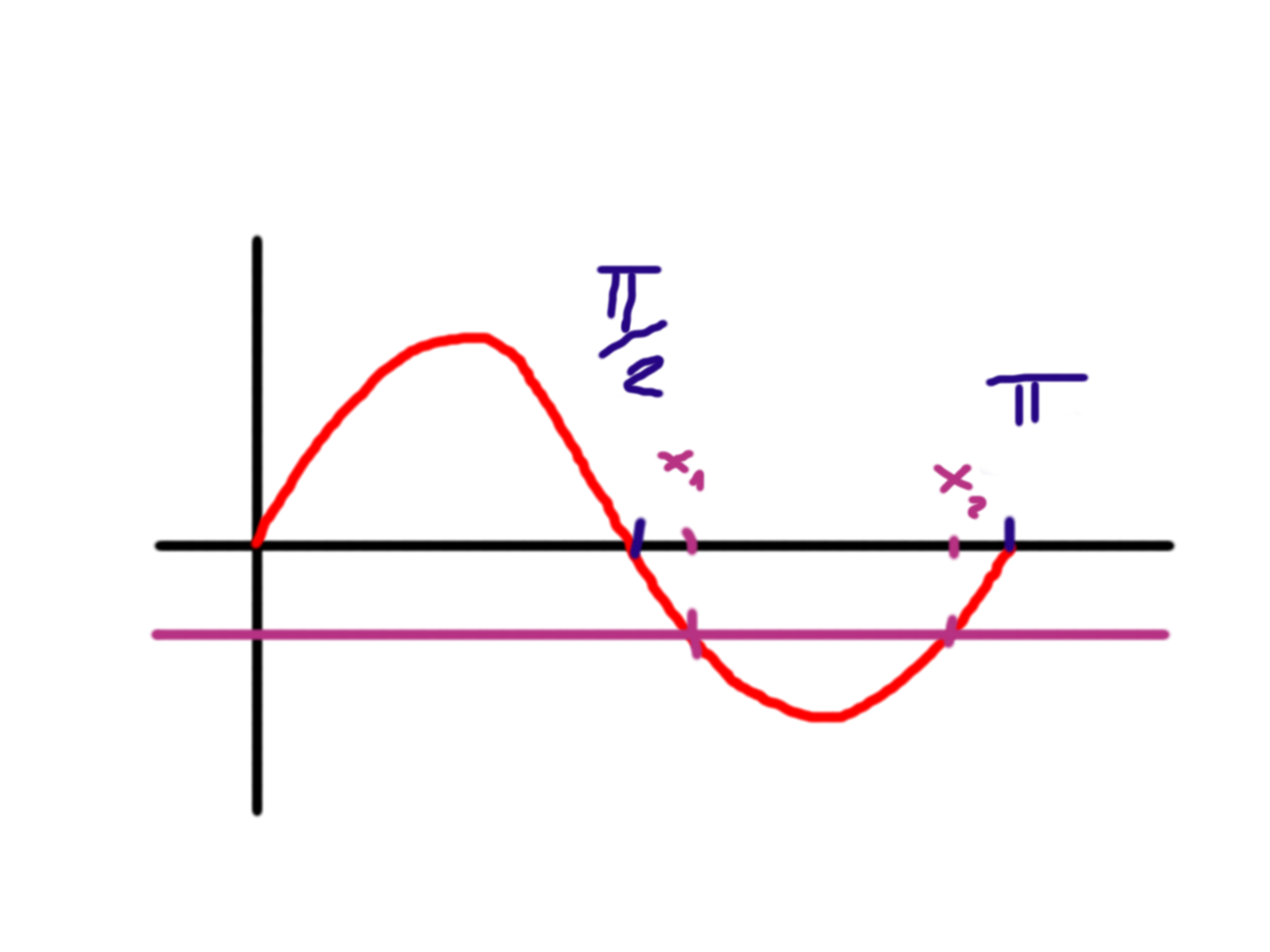
V obrázku jsem rovnou fialově naznačil čáru odpovídající hodnotě \(-\frac{\sqrt{3}}{2}\). A pokud napíšeme rovnici ve tvaru, který uvádím výše, tedy \(\sin 2x = -\frac{\sqrt{3}}{2}\), na co se takovou rovnicí vlastně ptáme?

Cílem je určit taková \(x\), která mají společné \(\sin 2x\) a ono číslo na pravé straně rovnítka. Co o takových \(x\) můžeme říci?

• Na našem rozsahu \(\lt 0 ; \pi \gt\) budou dvě (viz obrázek)
• Víme, že budou v druhé polovině křivky (tedy mezi \(\frac{\pi}{2}\) a \(\pi\)), čili “stupňově” mezi 90 a 180 (nikoliv 180 a 360, protože se jedná o dvakrát “rychlejší” křivku)

Správně si nastavíme kalkulačku (na výpočty ve stupních třeba) a zadáme “arkus sinus” pro hodnotu \(-\frac{\sqrt{3}}{2}\).

Ale pozor! Kalkulačka umí vyhodit pouze jednu hodnotu, čili musíme správně uvažovat! V mém případě vyhodila \(-60\). Vezměme tedy těch \(180\) stupňů, které jsou na konci a odčtěme \(60\). Vyjde tedy \(120\). A co ta druhá hodnota?

Jednoduše — v našem případě vidíme, že se jedná o symetrické řešení podle nejhlubšího bodu sinusovky. A jak daleko je 120 od 90? Stejnou vzdálenost najdeme i od 180 a máme vyhráno 😉

V mašem případě je to tedy \(30\) stupňů, čili \(180-30=150\) — a to je naše druhé řešení.

Ale tam rozhodně nekončíme! Proč? Jak víme, křivka jde “do nekonečna” — prostě dál a dál. Neexistuje tak pouze jedno či dvě řešení, existuje jich nekonečně mnoho. Tato řešení jsou si však podobná — stejně jako všechny sinusovky vypadají “stejně”. Musíme tedy napsat řešení “velmi obecně”, ale aby bylo jednoznačně definováno.

Víme, že křivka se opakuje každé \(\pi\), čili bychom mohli napsat, že stejně, jako existuje řešení “120”, tak existuje i \(120+\pi\). Nojo, jenže ono platí i řešení \(120+2\pi\) a další. Proto uděláme trik — řešení napíšeme ve tvaru:

$$x_1 = 120 + k\pi; k\in \lt 1..\mathbb{N}\gt$$

$$x_2 = 150 + k\pi; k\in \lt 1..\mathbb{N}\gt$$

A to je celé, tádydádydá 😉