Archiv rubriky: Nezařazené
Měření rychlosti radarem a Dopplerův jev
Nejspíše jste už někdy viděli někoho jet rychlostí ohrožující bezpečí na silnici. Policie se snaží počet takovýchto “bláznů” redukovat tím, že radary měří rychlost aut, které posléze pokutuje. Ale jak takové měření probíhá?
V článku o Dopplerově jevu jste se dočetli, co je to Dopplerův jev[1]Dále už jen DJ.. Zkráceně, co to je – určitě jste si všimli toho, že když kolem vás projíždí vlak, tak při přibližování se k vám se frekvence “jeho zvuku” zvyšuje (čili jde stále o vyšší a vyšší tón, jako když hrajete na klavíru na klávesy více a více vpravo) a hned jak se od vás začne vzdalovat, frekvence náhle poklesne (čili stále nižší a nižší tón, jako když hrajete na klavíru na klávesy více a více vlevo).
Ale jak víme, u aut není tento zvuk tak znatelný při nižších rychlostech a hlavně by se to tímto způsobem dost špatně měřilo.[2]Kvůli šumu z okolí a kvůli vysoké nepřesnosti měření frekvence zvuku na větší dálku. Přesto je policie schopna rychlost radarem změřit.
Jaké jiné vlnění ještě vydává auto? Vyzařuje světlo v infračervené oblasti (čehož využívá termovize, např. k vidění objektů ve tmě) a ve viditelné oblasti světla.[3]Jinak bychom to auto ani neviděli. Ale my nikdy nevíme, jakou barvu má auto “doopravdy” (v klidu vůči nám), takže nemůžeme vypočítat rozdíl frekvencí, tudíž ani rychlost.
Ale co když my sami budeme vysílat paprsky k pohybujícím se objektům? Vyšleme-li signál s určitou frekvencí (a tedy i vlnovou délkou podle vzorce \(f = \frac{c}{\lambda}\) )[4]Tento vzorec nám v podstatě říká, že se zvyšující se rychlostí za konstantní vlnové délky se frekvence zvyšuje a při zvyšující se vlnové délky za konstantní rychlosti se frekvence zmenšuje. k objektu, který se vůči nám pohybuje, frekvence signálu se díky pohybu auta bude měnit.
Tato frekvence bude ale tentokrát dvakrát posunuta. Jednak z toho důvodu, že se změnila vzdálenost během té doby, než se signál dostal k objektu (zmenšila, či zvětšila), a také
z toho důvodu, že došlo k odrazu a paprsek musel urazit ještě jednou tu samou cestu zpátky k radaru.
Odvození pro rovnoměrný přímočarý pohyb
Tedy vyšleme-li signál s frekvencí \(f\) proti objektu (autu), které se k nám přibližuje po přímce, tak se frekvence bude měnit takto:
$$ \ f_p = \frac {f_sc + f_sv_s}{c} $$
My chceme určit rychlost daného objektu, čili vyjádříme \(v_s\):
$$ \ v_s = \frac {f_pc – f_sc}{f_s}$$
Toto ale není ta rychlost, kterou nám naměří radar. Takhle by to platilo, kdybych věděl frekvenci vyslaného paprsku, v autě zjistil získanou frekvenci a z toho tímto vzorcem vypočetl rychlost.
Paprsek se ale ještě musí odrazit a vrátit zpátky, takže musí dojít k druhému posunu. Protože jsme “obrali” paprsek o jednu cestu z pohledu radaru, tímto vzorcem nám vyšlo \(2v_s\). Vzorec jen upravíme tak, že obě dvě strany vydělíme dvojkou a vyjde nám:
$$ \ v_s = \frac {f_pc – f_sc}{2f_s}$$
Nyní praktický příklad. Policejní radary využívají vlnění s velmi krátkou vlnovou délkou, tedy velice vysokou frekvencí. Rychlost vlnění je \(c\) – rychlost světla.[5]Obecně se do vzorce dosazuje rychlost jakéhokoliv vlnění, zde se “náhodou” \(c\) rovná rychlosti světla (která se jinak sama o sobě značí \(c\) ).
Běžně se frekvence vyslaného paprsku \(f_s = 10\ 600\ 000\ 000\ \mathrm {Hz}\). Uvažujme, že radar vyšle paprsek proti blížícímu se autu a vrátí se k němu frekvence \(f_p = 10\ 600\ 001\ 825.555555 \ \mathrm {Hz}\) (zde bohužel nemůžeme moc zaokrouhlovat, protože potřebujeme rychlost co nejpřesněji). Dosadíme do vzorce:
$$ \ v_s = \frac {10\ 600\ 001\ 825.555555\cdot 3\cdot 10^8-10\ 600\ 000\ 000\cdot 3\cdot 10^8}{2\cdot10\ 600\ 000\ 000} $$
Když toto napíšeme do kalkulačky, vyjde nám, že \(v_p = 25.833 \ \mathrm {m/s} = 93 \ \mathrm {km/hod}\)
93 kilometrů za hodinu se ještě toleruje (mimo obec) a policajt to nebude dále řešit.
V případě, že objekt (auto) se vzdaluje od radaru, frekvence se bude snižovat, takže v našem vzorci by nám vycházelo \(-v_s\), takže jen vydělíme obě strany minus jedničkou a vyjde:
$$ \ v_s = \frac {f_sc – f_pc}{2f_s}$$
Oba tyto takto platí jen tehdy, když se ode mě auto pohybuje přímo po přímce, příště už se konečně vrhneme na již dříve slibovaný vzorec, kdy se zdroj (nebo pozorovatel) pohybuje po různých křivkách. Hezký den! 🙂
Poznámky pod čarou
| ⇧1 | Dále už jen DJ. |
|---|---|
| ⇧2 | Kvůli šumu z okolí a kvůli vysoké nepřesnosti měření frekvence zvuku na větší dálku. |
| ⇧3 | Jinak bychom to auto ani neviděli. |
| ⇧4 | Tento vzorec nám v podstatě říká, že se zvyšující se rychlostí za konstantní vlnové délky se frekvence zvyšuje a při zvyšující se vlnové délky za konstantní rychlosti se frekvence zmenšuje. |
| ⇧5 | Obecně se do vzorce dosazuje rychlost jakéhokoliv vlnění, zde se “náhodou” \(c\) rovná rychlosti světla (která se jinak sama o sobě značí \(c\) ). |
Příklad pro Jarmilu
Příklad s goniometrickými funkcemi pro Jarmilu 🙂 Anebo jak dostat ze \(\sin 2x = -\frac{\sqrt{3}}{2}\) ono \(x\)? 🙂
Co nám tuto zadání vlastně říká? K řešení máme už veškeré podklady; víme, jak vypadá graf funkce \(\sin x\), jak však vypadá graf funkce \(\sin 2x\)?
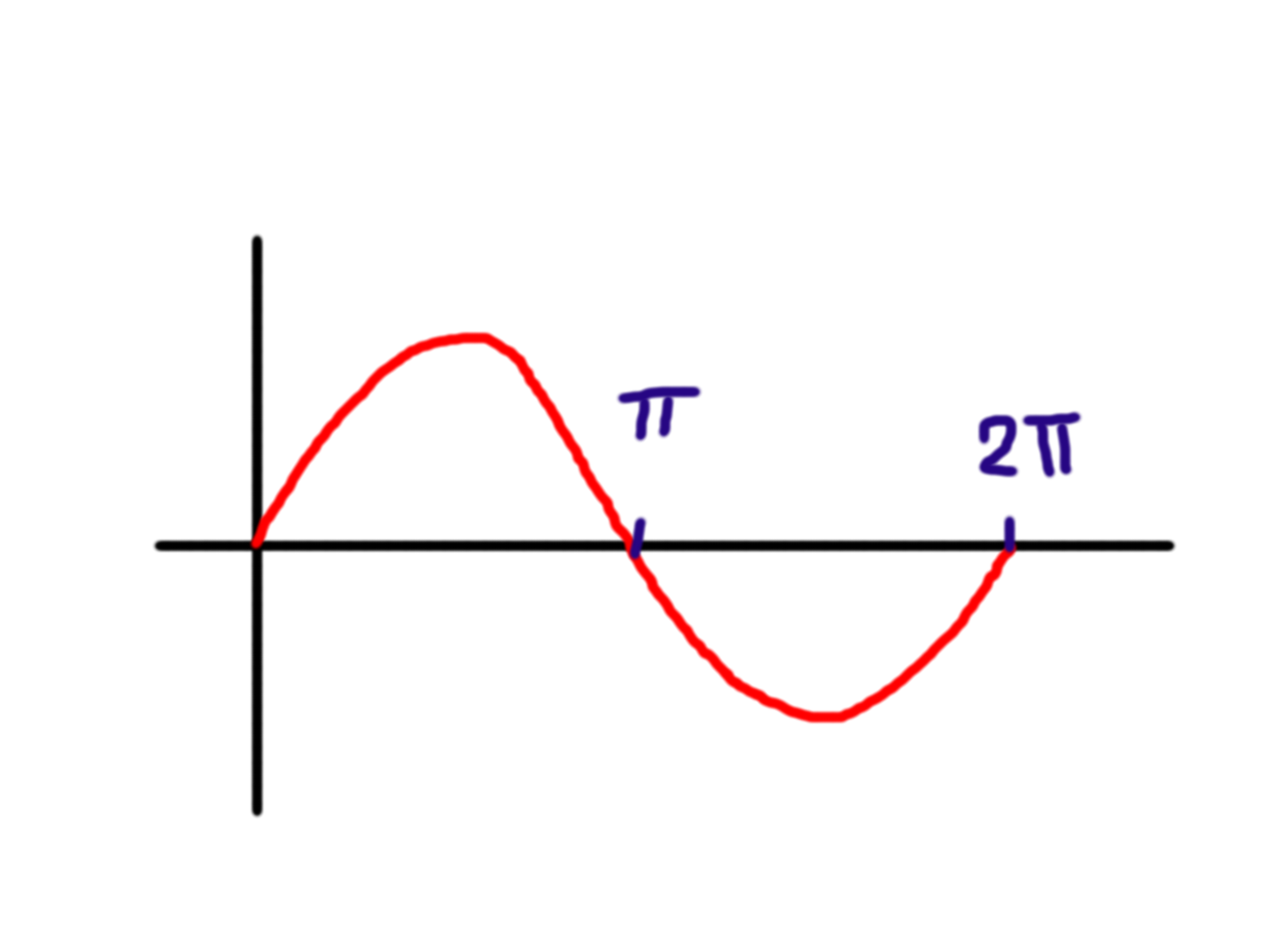
Výchozí funkce \(y(x)=\sin x\) tedy vypadá takto:
Funkce \(y(x) = \sin 2x\) vypadá úplně stejně, akorát má dvakrát větší frekvenci, což znamená totéž, jako když řeknu, že má dvakrát menší periodu. Křivka tak necestuje od \(0\) do \(2\pi\), ale jen do \(\pi\).
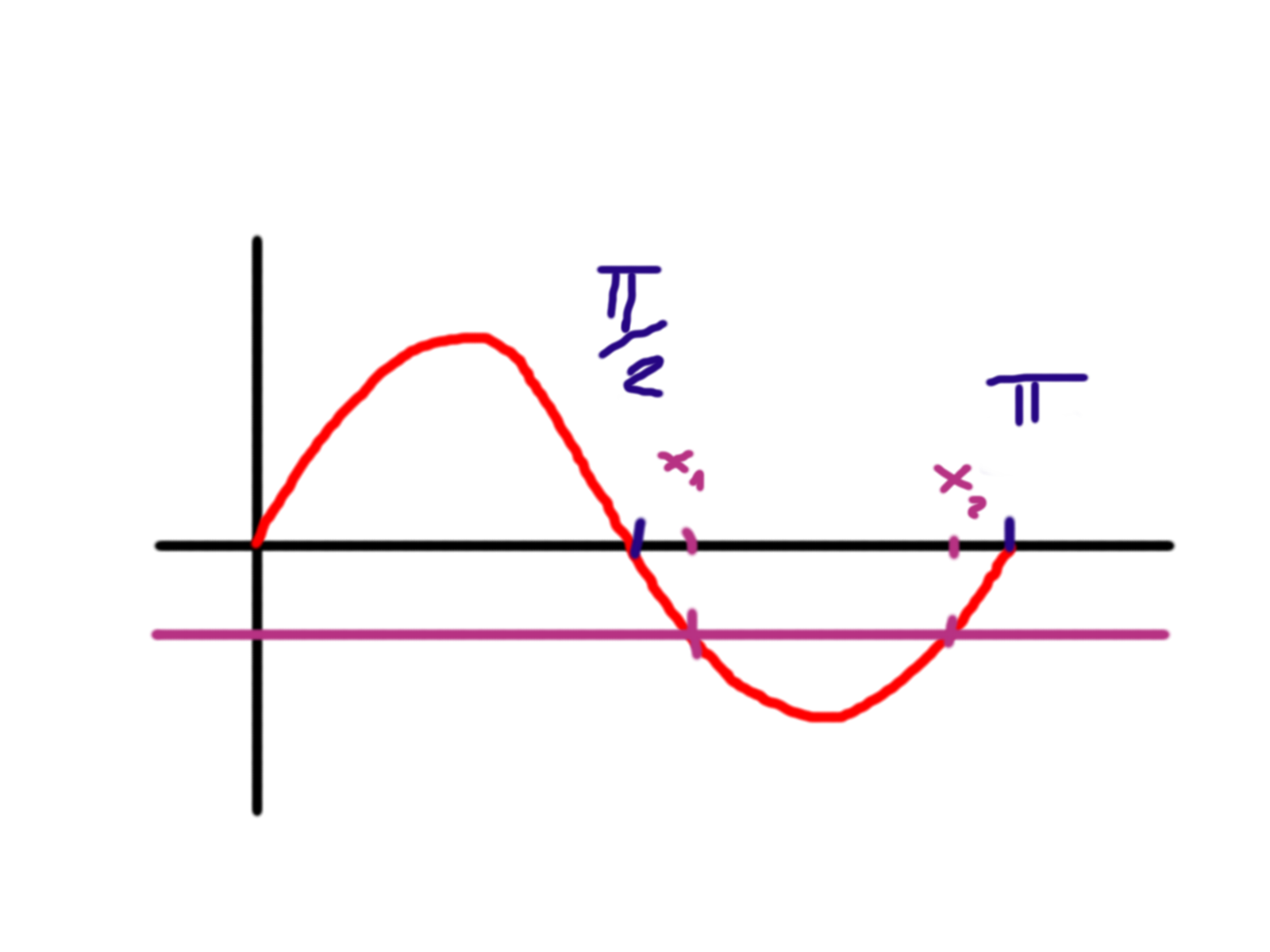
Vypadá to tedy nějak následovně:
V obrázku jsem rovnou fialově naznačil čáru odpovídající hodnotě \(-\frac{\sqrt{3}}{2}\). A pokud napíšeme rovnici ve tvaru, který uvádím výše, tedy \(\sin 2x = -\frac{\sqrt{3}}{2}\), na co se takovou rovnicí vlastně ptáme?
Cílem je určit taková \(x\), která mají společné \(\sin 2x\) a ono číslo na pravé straně rovnítka. Co o takových \(x\) můžeme říci?
- Na našem rozsahu \(\lt 0 ; \pi \gt\) budou dvě (viz obrázek)
- Víme, že budou v druhé polovině křivky (tedy mezi \(\frac{\pi}{2}\) a \(\pi\)), čili “stupňově” mezi 90 a 180 (nikoliv 180 a 360, protože se jedná o dvakrát “rychlejší” křivku)
Správně si nastavíme kalkulačku (na výpočty ve stupních třeba) a zadáme “arkus sinus” pro hodnotu \(-\frac{\sqrt{3}}{2}\).
Ale pozor! Kalkulačka umí vyhodit pouze jednu hodnotu, čili musíme správně uvažovat! V mém případě vyhodila \(-60\). Vezměme tedy těch \(180\) stupňů, které jsou na konci a odčtěme \(60\). Vyjde tedy \(120\). A co ta druhá hodnota?
Jednoduše — v našem případě vidíme, že se jedná o symetrické řešení podle nejhlubšího bodu sinusovky. A jak daleko je 120 od 90? Stejnou vzdálenost najdeme i od 180 a máme vyhráno 😉
V mašem případě je to tedy \(30\) stupňů, čili \(180-30=150\) — a to je naše druhé řešení.
Ale tam rozhodně nekončíme! Proč? Jak víme, křivka jde “do nekonečna” — prostě dál a dál. Neexistuje tak pouze jedno či dvě řešení, existuje jich nekonečně mnoho. Tato řešení jsou si však podobná — stejně jako všechny sinusovky vypadají “stejně”. Musíme tedy napsat řešení “velmi obecně”, ale aby bylo jednoznačně definováno.
Víme, že křivka se opakuje každé \(\pi\), čili bychom mohli napsat, že stejně, jako existuje řešení “120”, tak existuje i \(120+\pi\). Nojo, jenže ono platí i řešení \(120+2\pi\) a další. Proto uděláme trik — řešení napíšeme ve tvaru:
$$x_1 = 120 + k\pi; k\in \lt 1..\mathbb{N}\gt$$
$$x_2 = 150 + k\pi; k\in \lt 1..\mathbb{N}\gt$$
A to je celé, tádydádydá 😉