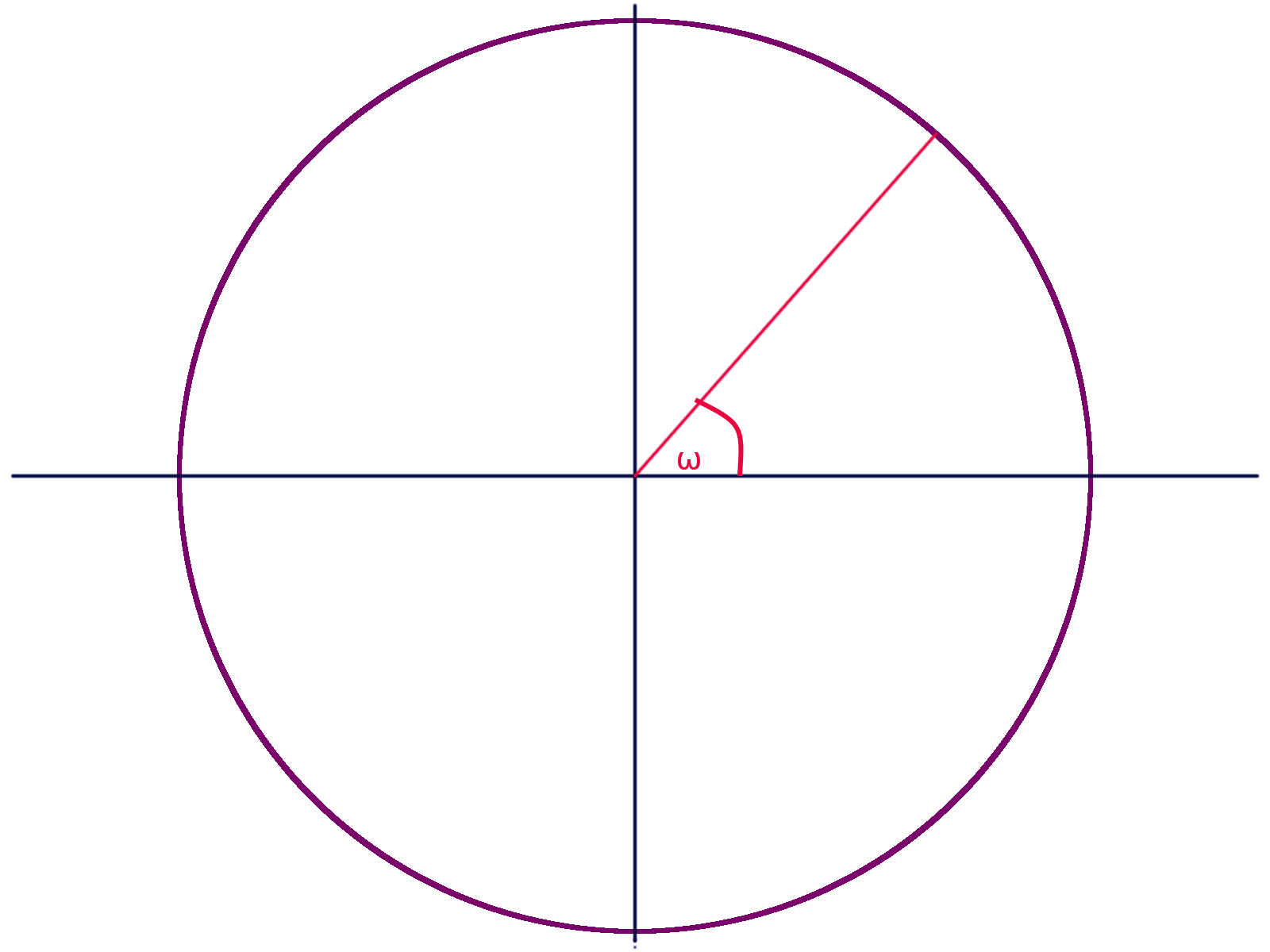
Kamarád (Pavel Kachlíř) se mě zeptal, jestli je možné, že zobrazení laseru na kruhové podložce může být rychlejší, než \(c\), pokud budu laserem dostatečně rychle hýbat. Použil k tomu následujícího situačního obrázku:

Rychlá odpověď — ano, průmět laseru se může pohybovat rychlostí \(> c\). Nicméně nyní proč:

Uvažujme samzořejmě (pro zjednodušení), že rychlost šíření laseru je právě \(c\), tedy rychlost světla. Samozřejmě si dokážeme představit, že z dotyčného situačního obrázku se intuitivně dokážeme dostat do stavu, kdy aniž by se laser pohyboval rychlostí větší než \(c\), jeho obrázek se takovou rychlostí pohybovat může.

Celý problém tkví v tom, co nám říká relativita^[1]STR — speciální teorie relativity — stručně řečeno, že žádná informace, částice či předmět obecně se nemůže pohybovat rychlostí, která by dosáhla rychlosti \(c\), tedy že jakákoliv rychlost pohybu v prostoru musí být \(v < c\). Rychlost \(c\) je tedy nedosažitelná.

Překresleme si trošku sitauční plánek, využijme úhlové rychlosti a rychlosti pohybu:

Začněme tedy jednoduše — mějme takovouto situaci, kdy ve středu kruhu máme laser, který se otáčí nějakou rychlostí \(\omega\):

Další důležitou informací pro nás bude poloměr kruhu, v našem případě tedy \(r\):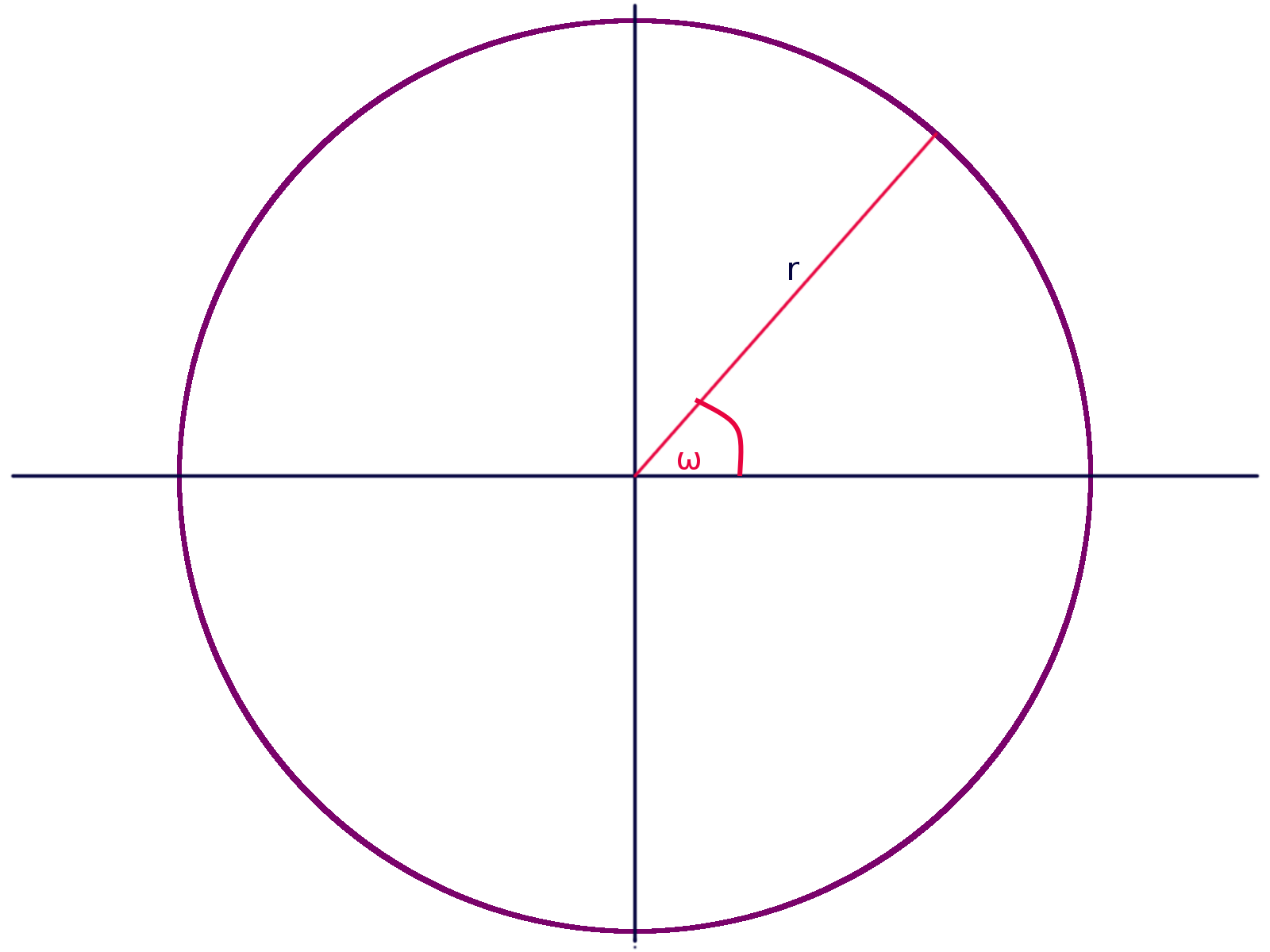

A nyní se ptáme: Jak závisí doba přenosu laseru ze středu soustavy na okraj? Odpověď přece známe — víme, že:

$$s = v t$$

čili

$$t_{\phi} = \frac{s}{v} = \frac{r}{c}$$

Protože se jedná o kruh, tato doba bude stále konstantní, ať už bude laser natočený kamkoliv.

Nyní si napišme rovnici:

$$\phi =  A \sin \left(\omega t + \phi_0\right)$$

Kde \(\omega t\) je úhlová rychlost pohybu, \(A\) je amplituda, tedy \(r\) a \(\phi_0\) je nějaký fázový posuv, který v našem případě bude záviset na \(t_{\phi}\), které jsme si vyjádřili výše.

Jak ale závisí? Víme, že doba, kterou signál (paprsek) potřebuje na uražení vzdálenosti laser–obvod bude \(t_\phi\), čili než tam signál doletí, laser se otočí o \(\omega t_\phi\). Čímž máme jasně daný fázový posuv a můžeme psát:

$$ \phi = r \sin \left(\omega t + \omega \frac{r}{c}\right)$$

Musíme však uvažovat, že signál se bude zpožďovat a ne předbíhat, musíme tedy psát:

$$ \phi = r \sin \left(\omega t – \omega \frac{r}{c}\right) $$

Pokud si za \(\omega\) nyní dosadíme takovou frekvenci, kdy by se změna \(\frac{\phi}{t}\) měla odehrávat rychleji, než \(c\), nic se nestane 😉 Bude docházet samozřejmě k fázovému zpoždění, ale samotné zobrazení (projekce) světla laseru se může zdánlivě pohybovat \(v>c\).