Vítám vás u pokračování tématu o polarizaci a spinu částic. V prvním díle jsme zlehka naznačili matematický aparát a obecné principy, v tomto článku jich dále budeme využívat, proto pokud budete potřebovat, velmi doporučuji otevřít si první článek a v případě matematických nejasností zde se na něho odkazovat, mělo by tam být vysvětleno vše důležité.
Archiv autora: Rudolf Klusal
Polarizace a spin částice (1. část)
V minulém článku o Entropii a termodynamice jsem vám slíbil, že se zase vrátíme zpět k “nějakým částicím”. Nevrátíme se však k nějakým konkrétním, vrátíme se totiž pouze k jedné z jejich vlastností — spinu.
Ohledně spinu existuje takový problém — on se (jako vlastnost) dá jen velmi těžko představit. Můžu samozřejmě používat různých analogií, ale jak si ukážeme, když se trošku ponoříme do problematiky, dost těchto analogií (buďme upřímní — všechny) ukážou dříve či později nějaký zásadní smrtelný problém. Jak už je však zvykem, než se dáme do samých popisů spinů částic a jak s nimi fungovat, musíme si připravit lehké matematické podhoubí, abychom pochopili zákonitosti[1]Protože pokud chceme pochopit spin, musíme pochopit i ten zbytek..
Pokračování textu Polarizace a spin částice (1. část)
Poznámky pod čarou
| ⇧1 | Protože pokud chceme pochopit spin, musíme pochopit i ten zbytek. |
|---|
Temná energie
Abychom se mohli podívat na temnou energii, musíme uvést alespoň pár věcí na pravou míru. Nejprve — co to vůbec taková temná energie je a jakým způsobem vůbec víme, že něco takového s nejvyšší pravděpodobností bude existovat.
Když E. Hubble v roce 1923 rozšířil hranice nám známého vesmíru a potvrdil (pozorováním a měřením vzdáleností), že mlhovina v Andromedě není jen nějaká další mlhovina, ale celá galaxie, která je navíc několikrát větší než naše Galaxie, nutně narazil na pár poznatků, které doslova otřásly dosavadní vědeckou komunitou a přidaly další pilíře poznání vesmíru a tedy i světa kolem nás.
Jedním z těchto pilířů bylo i objevení faktu, že vesmír se rozpíná. Všiml si totiž, že vzdálenější galaxie se od té naší vzdalují rychleji než ty bližší a usoudil z toho, že prostor doslova “vzniká” mezi těmito galaxiemi .
Chráněno: Úlohy pro D
Motor — jak je to s výkonem a momentem?
Na základě diskuse na Facebooku, kde se kamarád pokoušel pochopit z mých krátkých příspěvků, jak souvisí výkon a kroutivý moment, jsem se raději rozhodl sepsat myšlenky do plnohodnotného (byť krátkého) článku. Zcela věřím, že totiž tento kamarád nebude jediný, kdo má v uvedených pojmech jakousi “mlhu” a potřeboval by je osvětlit.
Výkon, kroutivý moment a jejich význam
Všechny motory máme na světě proto, aby konaly nějakou práci. Práce, uváděná v Joulech, je veličina, která nám popisuje doslova “kolik je toho třeba udělat”. Kupříkladu pokud budeme táhnout 500kilový klavír do 4. patra, tedy zhruba do 20 metrů výšky, budeme potřebovat přibližně (zaokrouhlujme prosím) práci:
$$W=F s = m g s = 500 \cdot 10 \cdot 20 = 100\ \mathrm{kJ}$$
(ke stejnému výsledku bychom došli, kdybychom počítali přes potenciální energii, kde \(W = mgh\), což je vlastně totéž v našem případě 😉 )
Abychom tedy dostali takový klavír do takového 4. patra, potřebujeme někde sehnat práci \(100\ \mathrm{kJ}\). Buď ji vyvineme ručně, kladkami či použijeme nějaký motor. Jenže samozřejmě intuitivně, pokud budeme mít motor, který bude mít “větší páru”, vytáhne nám tam klavír mnohem rychleji než nějaký slaboučký motůrek. Množství toho, jakou “to má páru” se tedy říká výkon a jedná se velmi jednoduše po schopnost provést nějakou práci za průměrný čas. Pokud bychom tedy chtěli náš klavír vytáhnout za 10 vteřin, budeme potřebovat výkon:
$$ P = \frac{W}{t} = \frac{m g s}{t} = \frac{500 \cdot 10 \cdot 20}{10} = 10\ \mathrm{kW}$$
Budeme tedy potřebova motor s výkonem alespoň \(10\ \mathrm{kW}\). Samozřejmě nebudeme uvažovat, že motory nemají 100% účinnost a tak podobně, spíše jde o princip jako takový.
Nicméně — je vám asi jasné, že úplně “nefunguje” jednoduchá zkratka, že pokud vezmu třeba motorek z ostřikovačů a budu s ním zvedat takový klavír, bude mi to trvat třeba 2 hodiny a zvednu ho. Samozřejmě by to mohlo fungovat, ale je potřeba, aby — byť pomalý — motor uměl vykonávat nějakou sílu, která by byla větší, než síla působící gravitací (tedy aby klavír neklesal, ale stoupal).
Musí být tedy schopen vyvinout určitý moment, kterým by na dané těleso působil (byť pomalu). Jedná se o točivý stroj (motor se otáčí a dělá pořád dokola to samé — zabírá), veličina, která nám popisuje toto silové působení se nazývá kroutivý moment.
Pokud definujeme dráhu, kterou musí obvod točivého stroje (jeho aktivní části) vykonat, aby udělal jednu otáčku, je to klasický obvod:
$$o=\frac{2\pi o}{60}$$
Šedesáti dělíme proto, že otáčky se uvádí v “rpm”, tedy “otáčkách za minutu”. Pokud máte otáčky v otáčkách za sekundu, poté samozřejmě nedělíte 🙂 Práce, jak víme, je silové působení po nějaké dráze, tedy:
$$ W = F s$$
No a pokud víme, že dráha je rovna obvodu:
$$ W = F s = F \frac{2 \pi r}{60}$$
Což je náš vztah pro výkon. Můžeme udělat zkratku, že:
$$M = F r$$
A tedy
$$ W = \frac{2 \pi M o}{60}$$
Daný výkon motoru tedy přímo souvisí s kroutivým momentem, kterým motor na danou “překážku” působí.
Praktické otázky
Vidíme, že výkon motoru je přímo závislý na otáčkách motoru. Zkusme si proto zaexperimentovat s různými průběhy kroutivého momentu a výkonu.
Příklad 1) Plochý “kroutivý moment”:
Průběh kroutivého momentu tedy bude vypadat např. takto:
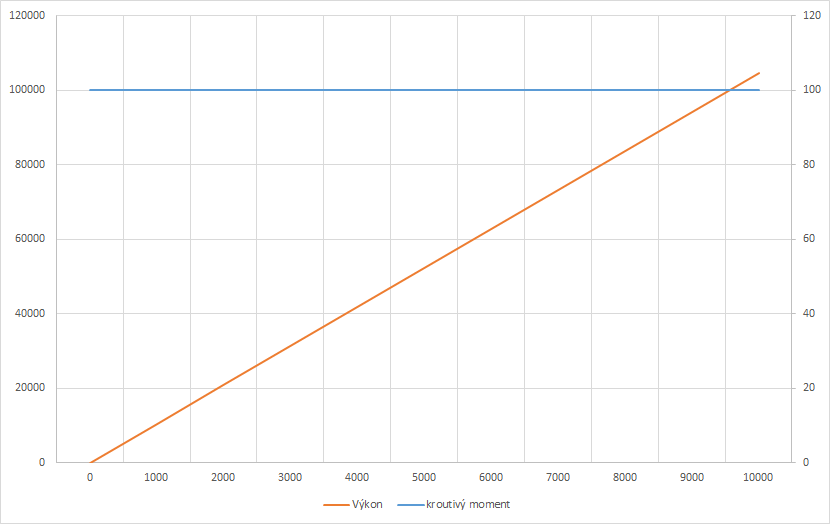
Vidíme, že motor, který by měl takto rovný průběh, by dosahoval největších výkonů při nejvyšších otáčkách, přičemž by měl stále konstantní kroutivý moment, v našem případě \(100\ \mathrm{Nm}\). Osa výkonu je ve Wattech, tedy vidíme, že kolem 10 000 otáček by měl motor výkon přes 100 kW, což odpovídá zhruba 135 koňským silám.
Žádný motor však nemá takto krásný průběh krouťáku, možná tak v Tesle se přibližují, ale jinak se jedná většinou o nějakou křivku. V technických specifikacích motoru většinou najdete, že máte “maximální krouťák” třeba 110 Nm při 4500 otáčkách. To znamená, že všude jinde je to “méně”. Zkusme si tuto situaci opět načrtnout grafem:
Příklad 2) Motor s reálným krouťákem
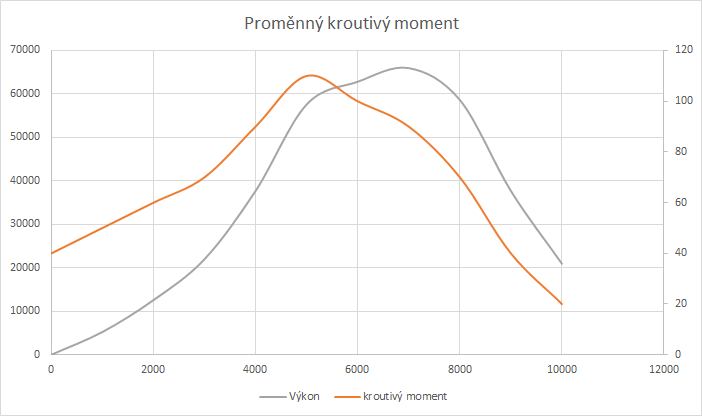
Zde vidíme zajímavý jev — zatímco kroutivý moment má svůj vrchol zhruba v oněch 5000 otáčkách, výkon má svůj vrchol skoro až v 7000. Tyto charakteristiky jsou právě velmi důležité — čím máte vyšší krouťák ve vyšších otáčkách, tím máte i větší výkon.
Doufám, že je to vše jasné, případně se ozvěte do komentů 😉 A budu rád za sdílení! 😉
Chemtrailisti jsou idioti :-)
Dostal jsem se poměrně omylem k článku pro chemtrailisty a chtěl bych ho rozebrat 🙂
V prvním odstavci se tazatel ptá: “Kolik více důkazů ještě potřebujeme, než bude většina populace ochotna čelit faktu, že jsme práškováni vysoce toxickými látkami, které jsou součástí programu klimatického inženýringu?”
Má odpověď: Stačil by jediný 🙂
“motory s vysokým stupněm turbofanu (standardní pro všechny komerční dopravce a všechny armádní tankerové stíhačky) jsou svým designem téměř neschopny produkce kondenzační stopy.“
Toto není pravda. Tvorba kondenzační stopy závisí na použité technologii pouze okrajově, všechny proudové motory tvoří kondenzační stopu v momentě, co vznikne kondenzační ložisko ve vzduchu, který motorem prochází. Což je v každém motoru, protože žádný proudový motor není bez emisí.
“85% vzduchu, který prochází tímto motorem, není spalováno.“
Ano, souhlasím 🙂 Dokonce více, řekl bych, že možná tak 100 % 🙂 Vzuch totiž není v motoru spalován vůbec, pouze kyslík ze vzduchu.
“Sečteno a podtrženo, komerční dopravní letadla jsou vybaveny rozprašovacími tryskami, upevněnými na pylonu, přímo v jedné přímce s přítlakovým proudem stíhačkového motoru. “
Totálně nesmyslná věta, vůbec ji nechápu 🙂
Poté se v článku vyskytuje hromada fotografií letadel a jejich motorů, které vypadají naprosto normálně, vidíme klasické odtrhové de-ice hrany, výfuky, klapky a ovládací plochy na křídlech.
Nic víc tam nevidím, jen spousta blábolů od duševně nemocných lidí. Lidí, kteří mají volební právo. Lidí, kteří mohou chodit mezi námi a třeba učit naše děti ve škole.
Výška hladiny po vložení kostky ledu do vody
Tento příklad je velmi jednoduchý, nicméně stojí za uvedení:
Zadání (překopírované z Facebooku zní): V nádobě o podstavě s hranami 10 cm a 15 cm je přesně 1 litr vody v kapalném stavu. Do kapaliny je vhozena krychle vodního ledu o hraně 4 cm. Jaká bude výška hladiny ihned potom, co se hladina po vhození ledové kostky ustálí? Jaká bude výška hladiny potom, co se kostka rozpustí? Pro jednoduchost předpokládejme hustotu kapalné vody \(1 \frac{g}{cm^3}\) a ledu \(\frac{9}{10} \frac{g}{cm^3}\), a žádné závislosti objemu na teplotě.
Víme, že objem bude tedy:
$$V = a b v$$
kde \(v\) odpovídá výšce. Z toho snadno určíme:
$$v = \frac{V}{ab}$$
Nyní musíme zjistit vliv vložené kostky. Objem takové kostky je:
$$V = 4^3$$
Podle Archimédova zákona bude plavat a vytlačí množství vody v poměru hustot, tedy vytlačí:
$$V_{vytlaceno}=V_{led} \frac{\rho_{led}}{\rho_{voda}}$$
Tedy výsledná výška bude:
$$v = \frac{V_{vytlaceno}+V}{ab}$$
Dosadíme tedy:
$$v = \frac{V_{led} \frac{\rho_{led}}{\rho_{voda}}+V}{ab}=\frac{4^3\frac{9}{10}+1000}{10 \cdot 15} = 7,051\ \mathrm{cm}$$
Před vytlačením tedy nebyl objem s ledem:
$$v = \frac{V}{ab}=\frac{1000}{10 \cdot 15} = 6,667\ \mathrm{cm}$$
Rozdíl je tedy necelé \(4\ \mathrm{mm}\).
UPDATE: Jsem si všiml, že jsem zadání špatně opsal (celý já), základna je čtvercová o hraně 10 cm — nicméně to není problém, to se snadno dosadí do vzniknuvších vztahů a vyjdou výšky \(10,576\ \mathrm{cm}\) a \(10\ \mathrm{cm}\), tedy rozdíl zrhuba necelých 6 milimetrů 😉
UPDATE 2: Zapomněl jsem ještě na část řešení — jak se změní hladina poté, co se led rozpustí. Logicky — nezmění, hmotnost ledu a hmotnost vody po rozpuštění kostky bude stejná, tedy vytlačí se stejné množství.
Studna a dva klacky
Dostal jsem od instruktora v autoškole velmi zajímavý příklad — pokud ho znáte, tím lépe, ale fakt jsem ho neznal a hodně se mi líbil, zkusil jsem tedy přijít na nějaké řešení 😉 😉 Nakonec mi z toho “vypadlo” něco normálního (tedy reálného), svůj postup tedy uveřejňuji zde.
Mějme následující zadání: Existuje studna neznámé hloubky a průměru, do které hodíme dva klacky; jeden třímetrový, druhý dvoumetrový. Předpokládejme, že jsou “v rovině” a jejich místo setkání je nad dnem studny ve výšce 1 metr. Otázka zní — jaký je průměr takové studny.
Situační obrázek bych navrhl asi takto:
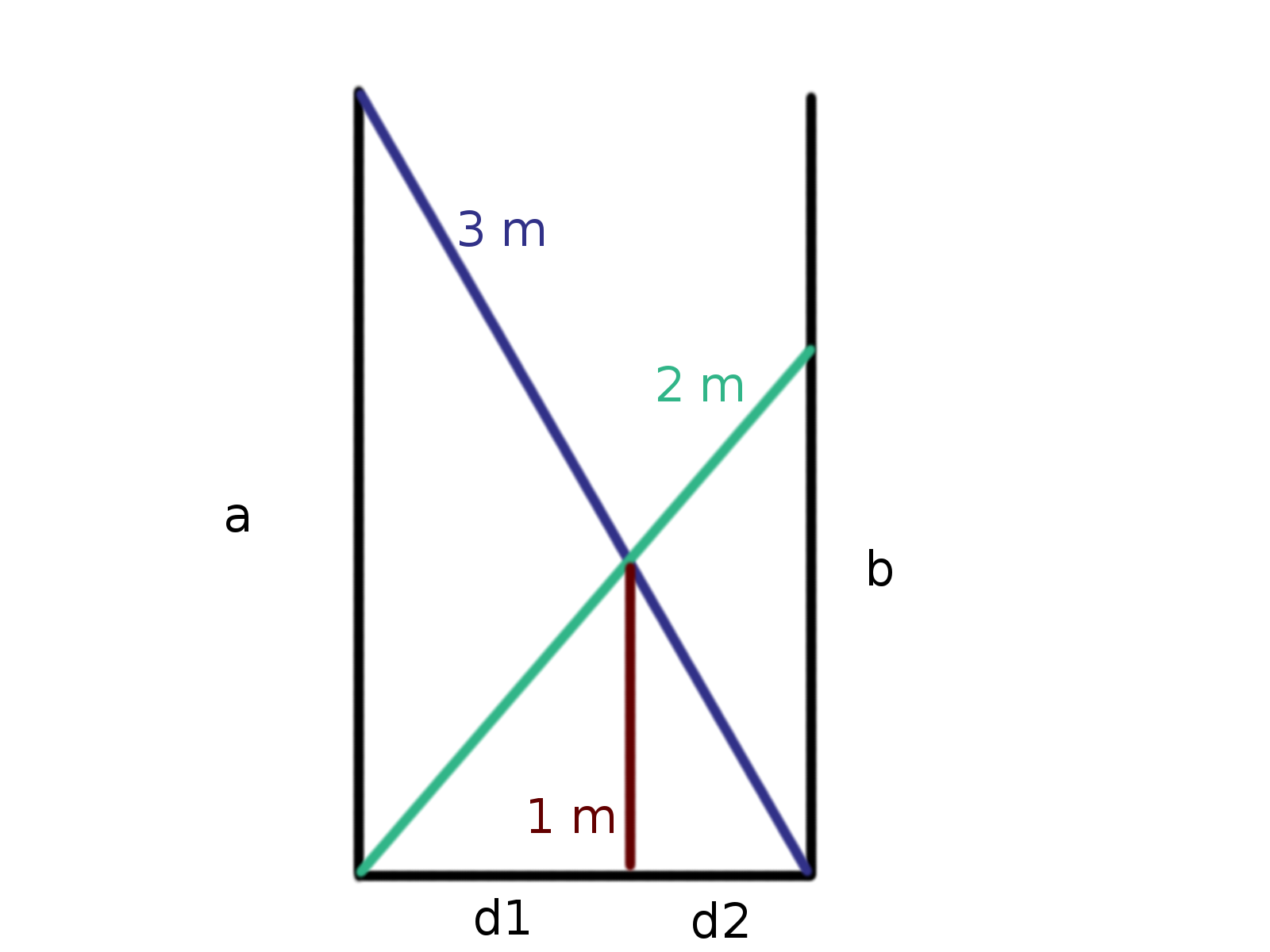
Začal bych asi svojí první myšlenkou, a to sice že řešení se určitě bude dělat nějak přes podobnosti trojúhelníků. Začal jsem tedy zuřivě hledat různé podobnosti, některé mě zavedly do slepých cest (tedy ne, že by si některé trojúhelníky nebyly podobné, ale bylo mi to k ničemu), ale nakonec se jedna cesta zadařila, tu zde i prezentuji 🙂
Ze všeho nejdříve si napíšeme rovnice, ze kterých budeme vycházet. Jedné se o soustavu různě propletených pravoúhlých trojúhelníků. Ze všeho nejdříve si určeme, že celkový průměr \(d\) bude samozřejmě roven:
$$d = d_1+d_2$$
A nyní můžeme pracovat s jednotlivými stranami:
$$\begin{array} aa^2+d^2 & = & 3^2 \\ b^2 + d^2 & = & 2^2\end{array}$$
Tím jsme popsali dva hlavní (velké) trojúhelníky. Nyní popíšeme vztahy v trojúhelníku s naznačenou výškou. Vyjdeme právě z té podobnosti, tedy že:
$$\frac{d_1}{v} = \frac{d}{b}$$
tedy po dosazení \(v=1\) získáme:
$$d_1 = \frac{d}{b}$$
a obdobně
$$d_2 = \frac{d}{a}$$
Vyjádříme si jednu a druhou stranu:
$$d_1=\frac{d}{b}, d_2=\frac{d}{a}$$
a dosadíme do výše uvedené rovnice součtu částí průměru:
$$d=\frac{d}{b}+\frac{d}{a}$$
Z toho vyjádříme jednu či druhou proměnnou, začněme třeba \(a\):
$$\frac{d}{a}=d-\frac{d}{b}=\frac{db-d}{b}$$
z toho tedy:
$$a = \frac{b}{b-1}$$
případně
$$b = \frac{a}{a-1}$$
Toto dosaďme do úplně prvních dvou rovnic pro velké trojúhelníky:
$$d^2+\frac{b^2}{\left(b-1\right)^2}=3^2$$
$$d^2+b^2=2^2$$
Vyjádříme si z druhé rovnice \(d^2\) a dosadíme do první:
$$2^2-b^2+\frac{b^2}{\left(b-1\right)^2}=3^2$$
Převedeme na rozumný tvar a vyřešíme jako rovnici 4. řádu, třeba pomocí Wolframu, to už je jedno (ale můžete zkusit ručně) a vyjdou 4 řešení, z toho 2 komplexní, která rovnou zavrhneme.
$$b_1=0,7009 ; b_2=1,5761$$
Které vybrat? To zatím nevíme, každopádně pokud dosadíme do rovnice pro průměr a odmocníme, vyjdou nám (prozatím) dvě řešení:
$$d_{I}=\sqrt{2^2-b_1^2} = 1,23$$
$$d_{II}=\sqrt{2^2-b_2^2} = 1,87316$$
Musíme vyjádřit tedy stejné rovnice, akorát pro vyjádřené \(b\), tedy:
$$b=\frac{a}{a-1}$$
Stejným postupem jako výše dostaneme rovnici:
$$3^2-a^2+\frac{a^2}{\left(a-1\right)^2}=2^2$$
a ta po vyřešení dá dva reálné kořeny:
$$ a_1=-2,34$$
$$a_2 = 2,7357$$
První rovnou vyhodíme, délky prostě záporné nechceme, držme se toho 🙂 Dosadíme tedy \(a_2\) a vyjde:
$$d=\sqrt{3^2-a_2^2}=1,2312$$
To se tedy shoduje s řešením “z druhé strany” problému — proto tento výsledek prohlásíme za finální. Průměr studny je tedy \(1,23\) metrů.
Jednoduché odvození Schrödingerovy rovnice
S kamarádem Lukášem jsme při čajově-matematicko-fyzikální rozcvičce zjistili, že už si nepamatujeme odvození Schrödingerovy rovnice 🙂 Pamatuji si, že jsme to kdysi ve škole dělali, musel jsem si to tedy oživit — a zde je má varianta toho, jak ji odvodit:
Nejdříve tedy vyjděme ze základních vztahů, jako vždy. Víme, že celková energie se dá popsat jako:
$$ E = E_k + E_p$$
kde \(E_k\) je kinetická a \(E_p\) je potenciální energie. Kinetickou energii můžeme přepsat klasicky jako:
$$ E = \frac{1}{2}mv^2 + E_p$$
a potenciální energii můžeme brát jako obecnou energii, ať už se jedná o energii vzniknuvší působením gravitačního, elektromagnetického či jakého pole; označme si ji dále \(u\). Finální forma tedy zatím budiž:
$$ E = \frac{1}{2}mv^2 + u$$
Dále se musíme podívat na vlny a vlnění jako takové. Vlnu můžeme jednoduše zapsat jako součet goniometrických funkcí v komplexní rovině:
$$ \Psi = \cos(kx-\omega t)+i\sin(kx-\omega t) $$
A exponenciální formě pak:
$$ \Psi = e^{i(kx-\omega t)} $$
Zderivujme dvakrát podle \(x\) a získáme (postupně):
$$ \frac{\partial \Psi}{\mathrm{d}x} = ik \cdot e^{i(kx – \omega t)} = ik \Psi$$
$$\frac{\partial^2 \Psi}{\mathrm{d}x^2}=(ik)^2e^{i(kx-\omega t)} = -k^2\Psi$$
Co je to \(k\)? Pokud si tak označíme “převod” mezi \(f\) a \(\omega\), potom \(k=\frac{2\pi}{\lambda}\) a tedy:
$$p=\frac{h}{\lambda}=\frac{hk}{2\pi}=\hbar k$$
a z toho plyne:
$$ k = \frac{p}{\hbar}$$
Dosadíme do rovnice s druhou derivací:
$$\frac{\partial^2 \Psi}{\mathrm{d}x^2}=-k^2\Psi = -\frac{p^2}{\hbar^2}\Psi = \frac{\partial^2\Psi}{\mathrm{d}x^2}$$
Přepíšeme-li si původní rovnici součtu energií: (vycházíme z faktu, že \(p=mv\), tedy \(p^2=m^2v^2\))
$$E = \frac{1}{2}mv^2 + u = \frac{1}{2m}p^2 + u$$
rozšíříme \(\Psi\):
$$E\Psi = \frac{1}{2m}p^2\Psi + u\Psi$$
a vidíme, že člen \(p^2\Psi\) se nám objevil i zde. Není tedy nic jednoduššího, než vytknout a dosadit:
$$E\Psi = \frac{-\hbar^2\partial^2\Psi}{2m\mathrm{d}x^2} + u\Psi$$
A to je tzv. časově nezávislá Schrödingerova rovnice. Časově nezávislá je proto, že se v ní prostě nevyskytuje \(t\), čas. Jak ho tam tedy dostat?
Víme, že \(E=hf\) a tedy:
$$E = hf = h\frac{\omega}{2\pi} = \hbar \omega$$
Vezměme původní vlnovou rovnici a zderivujeme, tentokrát podle \(t\):
$$ \Psi = e^{i(kx-\omega t)} $$
$$ \frac{\partial \Psi}{\mathrm{d}t}=-i\omega\Psi$$
$$E\Psi = -\hbar\omega\Psi$$
Podělíme \(\frac{-i}{k}\):
$$\frac{-i E \Psi}{k} = -i\omega\Psi = \frac{\partial \Psi}{\mathrm{d}t}$$
$$ E\Psi = \frac{\hbar\partial\Psi}{-i\mathrm{d}t}$$
a tedy
$$ \frac{-i\hbar\partial\Psi}{\mathrm{d}t}=E\Psi$$
Toto vzniknuvší \(E\Psi\) dosadíme do časově nezávislé rovnice a získáme:
$$\frac{-i\hbar\partial\Psi}{\mathrm{d}t}=\frac{-i\hbar^2\partial^2\Psi}{2m\mathrm{d}x^2}+u\Psi$$
A to je, vážení čtenáři, tzv. časově závislá Schrödingerova rovnice. 🙂
Níže mé ručně psané poznámky, třeba vám k něčemu budou 😉 😉
Hudba ve 432 vs 440 Hz
Tento článek nedávám ani do doplňkových článků, protože s fyzikou má společného fakt jen minimálně. Rovnou ho tedy dávám do “zábavy”. Nicméně pokud vám tato čísla nic neříkají, nejspíše patříte k té šťastné množině lidí, které průnik s množinou lidí, kteří věří či propagují tento nesmysl, je množina prázdná[1]Prostě jste o tom neslyšeli 🙂 .
O co se tedy jedná? Zastánci této podivné hypotézy říkají, že hudba je při podladění o 8 Hz příznivější tělu a mysli, než pokud se hraje v klasickém ladění. Možná by to však chtělo trošku alespoň fyzikálně zmínit, jak je to vlastně s laděním (když už se tedy máme bavit o fyzice).
Tóny
Asi to každý znáte — tón, zvuk, hluk; tyto termíny se definují snad už na ZŠ, čili nebudu je dlouho rozebírat, jen stručně: tón je na rozdíl od hluku homogenní a periodický, zvuk je množina všeho, do čeho patří i tón, hluk atp.
Jak víte, zvuk je mechanické vlnění nějakého prostředí, v našem případě vzduchu, které tímto přenáší nějakou zvukovou informaci. Tu pak mozek přes periferie (ucho) zpracovává na hudební či zvukový vjem.
Během historie se chápání “hudby” jako soustavy tónů poměrně dost bouřlivě vyvíjelo, nicméně to, že dnes používáme klasické tóniny, na které jsme zvyklí, není jen tak náhodou. Historii přenechám historikům, popíšeme si všechno pěkně fyzikálně.
Základní tón, harmonická, intervaly
Pokud vás zajímá více z hudební teorie, přečtěte si články, kde tyto věci popisuji (či případně články o itervalech) z hudebního hlediska, nicméně nyní pouze fyzikálně:
Jak jsme již řekli, tón je generován nějakým vlněním, v našem případě se omezíme na harmonické vlnění:
$$ f(t) = y = \sin \left(\omega t + \phi \right) $$
Kde \(y\) je aktuální výchylka, \(\omega\) je úhlová frekvence, \(t\) je čas, který do rovnice vstupuje jako parametr a \(\phi\) je fázový posuv. Nicméně pokud bychom si vytvořili např. takovýto tón, který má frekvenci 440 Hz, zněl by poněkud fádně, nezajímavě, nudně:
Krom toho, že tón není ani tak hlasitý a přesto je dost nepříjemný. Aby tón zněl lépe, je zapotřebí smíchat více tónů, nicméně ne jen tak ledabyle a náhodně, je potřeba je smíchat podle nějakých pravidel. Nejjednodušším mícháním je stav, kdy míchám různé “harmonické” frekvence. Co to je harmonická? Zde uvedený tón si můžeme zakreslit např. takto:

Jak vidíte, křivka se neustále opakuje — což je přesně to, co slovo “harmonická” znamená, je totiž periodická (tzn. neustále se opakující). Abychom mohli přidat třeba “druhou harmonickou”, musíme přidat takovou “harmonickou”, která bude mít stejné místo opakování — tedy aby tam, kde se křivka v nule[2]či tam, kam nás fáze posune potkává s osou \(t\), aby se i tam potkávala křivka další harmonické frekvence. Pokud přidáme např. frekvenci 880 Hz, tedy:

Výsledná frekvence bude prostým součtem těchto dvou křivek, tedy:
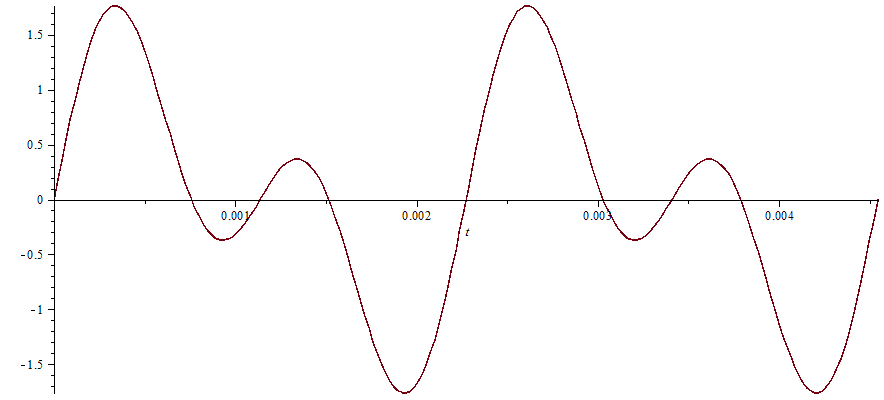
Sice už to není “sinusovka”, ale vidíme, že je to funkce neustále periodická. Zní nějak takto:
Kontrolní otázka (o další Fidorku!), pokud si tuten souzvuk pustíte, jak vysvětlíte ono “vlnění” zvuku? Proč zvuk nezní stále stejně, ale jako by pulzoval?
Nicméně tímto způsobem můžete přidat hromadu křivek, přidám ještě 220 a 110 Hz:

Vidíme, že křivka začíná být opravdu složitá, ale pořád je periodická, pořád se opakuje. Zní takto:
Nicméně když tento tón slyšíme, pořád je to prostě “takové jalové”. Jak se dosáhne toho, že tóny zní tak nějak lépe?
Zatím jsme totiž míchali pouze násobky harmonické — dvojnásobnou frekvenci, poloviční, čtvrtinovou. Tomuto intervalu mezi tóny se říká oktáva a vyjadřuje přesně to, co jsme si ukázali — dvojnásobek (či půlnásobek) původní frekvence. Pokud tón o frekvenci 440 Hz označíme jako \(a_1\), potom ten o frekvenci 880 Hz bude \(a_2\), frekvence 220 Hz odpovídá \(a\) a 110 potom \(A\) (čteme jako “á malé” a “á velké”).
To je však pořád jen tón A, ale kdo někdy viděl kytaru nebo klavír dobře ví, že je tam poněkud více tónů. Takže jak vzniknou? Začněme s další pěknou matematickou závislostí — čistou kvintou. Že je to kvinta, na to lidé přišli až později, nicméně kvinta má trojkové násobky. Smíchejme proto Náš tón 440 Hz s frekvencí 660 Hz, tedy \(\frac{3}{2}\) z 440 Hz:

Pro další intervaly platí další zákonitosti, nicméně takovýmto různým dělením dostaneme hromadu tónů, které když uspořádáme do našich známých stupnic, dostaneme tzv. Pythagorejské ladění, které tedy vznikne tím, že postupně přidáváme různé kvinty a posouváme je různě o oktávy nahoru a dolů. Nicméně dnešní nástroje nejsou laděny v Pythagorejském ladění, ale tzv. temperovaném, případně koncertním ladění.
Rozdíl mezi těmito laděními je mírně nad rámec fyzikálního článku, každopádně ve stručnosti — lidé si všimli, že pokud mírně posunou některé tóny, klavír bude třeba neustále “trochu rozladěn”, ale zase budou všechny tóny (současně hluboké a vysoké) k sobě ladit lépe. A právě takovému ladění se říká temeprované.
V článku o Fourierově analýze se můžete případně dočíst, jak je to se skládáním prakticky nekonečně mnoha různých frekvencí.
Zpět však k zastáncům “432 hypotézy”. Ti tvrdí, že pokud jako výchozí tón (tzn. vše ostatní je stejné) nepoužiji tón o frekvenci 440 Hz, ale 432 Hz, bude hudba příjemnější (s tím se dá i nedá souhlasit, záleží na skladbě), ale především že bude mít “pozitivní účinky na zdraví jedince”[3]Spíše tedy že “nebude mít negativní” účinky….
S argumenty této čtyři sta třicet dvojkové skupiny se dá poměrně slušně nesouhlasit; už jsem četl různé — od toho, že Mozart či Beethoven používali jiné ladění[4]Aby ne, když to bylo před staletími a moderní ladění se normalizovalo až kolem roku 1940., případně postují různé “pestrobarevné” obrázky s jakožemeditativní tématikou a vzájemně se poplácávají po zádech, jak to všem “čtyři sta čtyřicátníkům” nandali.
Názor si udělejte sami, případně zagooglete, že je to hloupost zjistíte po několika pročtených příspěvcích a studiích, nicméně nyní jen pro srovnání — stejný kousek písničky ve 440Hz ladění (tzn. beze změny) a ten samý kousíček se sníženým laděním (bohužel kvůli autorskému zákonu nemůžu více než 30vteřinovou ukázku):
Původní 440Hz verze:
“Vylepšená” 432Hz verze:
Jak slyšíme, “nějaký” rozdíl tam je. Nicméně vliv těchto změn je podle mého dost sporný. Často též vidíme různé obrázky, které tato skupina lidí posílá:

Je to sice krásné, ale netuším, proč by měla změna frekvence či toho, kde se různé harmonické potkávají, nějak ovlivňovat zdraví. Každopádně k výše uvedenému obrázku ještě pár slov:
Musíme totiž “probrat” ještě jeden typ vlnění, tzv. stojaté vlnění. To je narozdíl od postupného vlnění uvedeno “na místě”. Např. pokud klepnete do struny, ta se rozezní a bude “se vlnit” — stojaté vlnění. Vlna nikam necestuje, vlnové délky odpovídají různým poměrům délky struny. Postupné vlnění je takové, které pozorovatel vnímá jako vlnění až s tím, jak se věc, která se vlní, pohybuje — např. takový zvuk ve vzduchu. Vlny postupně jako kola po hození kamínku do vody cestují směrem od zdroje zvuku a pokud “narazí” na posluchače, ten je uslyší.
Nicméně stojaté vlnění má pár docela zajímavých vlastností — hráči na kytaru třeba ví, že pokud drknou na strunu tzv. flažolet tak, že ji rozezní jen “na půlce”, poté se druhá polovina struny rozezní též, akorát v opačné fázi 😉 Výsledná frekvence tónu bude tedy dvojnásobná, bude tedy o oktávu výše. Ale pokud si zkusíte takto rozeznít strunu třeba jen “o centimetr” vedle, už se tón neozve a vlnění okamžitě ustane.
Pokud bychom nakreslili obrázek toho, jak moc dobře struna zní, pokud v nějakém místě stiskneme strunu, dostaneme diagram, který je velmi podobný právě výše uvedným obrázkům (akorát ty berou osy jak X tak Y, v mém uvedeném případě se strunou by se aplikovala pouze osa X). Obrázky totiž zohledňují vliv prostředí, které celé kmitá — např. pokud jste v malé místnosti bez koberců, určitě slyšíte, že se zvuk tak podivně “nese” a rezonuje. A to přesně souvisí právě se stojatým vlněním — v některých frekvencích se vlny prostě nevyruší a budou znít déle a intenzivněji než v jiných.
Nicméně tato frekvence je naprosto závislá na rozměrech a tvaru místnosti. A stejně tak i výše uvedené obrázky, které mají simulovat vlnění na hladině vody — záleží kromě vstupní frekvence i na rozměrech misky či předmětu, který se vlní a kde toto vlnění zkoumáme.
Kdyby měli lidé své hlavy všechny stejně velké (tedy všichni lidé kdyby měli stejně velkou hlavu), samozřejmě by něco takového mohlo být zajímavé zkoumat. Bohudík tomu tak však není a každý si tak můžeme užívat jiného “vlnění”, které je nám příjemné.
Ohledně vlivu zvuku a frekvencí na tělo v biologickém slova smyslu opět požádám kolegu Lukáše, který se k tématu doufám též někdy vyjádří! 🙂

